 с прямым углом
с прямым углом  , EF — биссектриса
, EF — биссектриса  ,
,  , FG — искомый отрезок.
, FG — искомый отрезок.  .
.  — биссектриса, то
— биссектриса, то  (биссектриса
(биссектриса  делит
делит  на два равные угла).
на два равные угла). 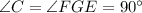 (это следует из условия: так как
(это следует из условия: так как  прямоугольный, то и
прямоугольный, то и  ; так как
; так как  — расстояние от
— расстояние от  до
до 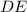 , то
, то 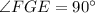 ).
).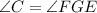 и
и 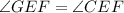 , то и третий угол первого треугольника равен третьему углу второго треугольника:
, то и третий угол первого треугольника равен третьему углу второго треугольника:  . Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так:
. Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так: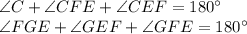
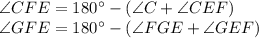
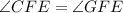 .
.  является для обоих треугольников общей.
является для обоих треугольников общей. (второй признак равенства треугольников — по стороне и двум прилежащим к ней углам (
(второй признак равенства треугольников — по стороне и двум прилежащим к ней углам ( — сторона, а
— сторона, а  — два прилежащих угла)).
— два прилежащих угла)). соответствует
соответствует  , тогда:
, тогда: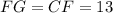
 . Смотрите второй рисунок.
. Смотрите второй рисунок.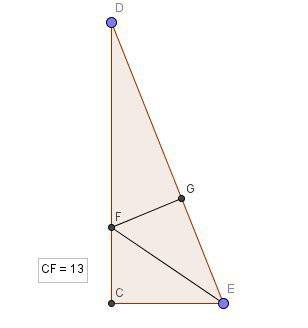
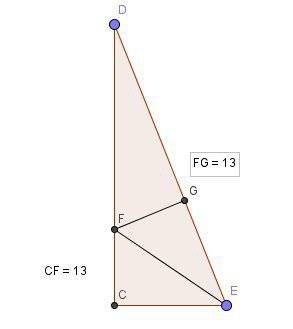
(x/3)^2+y^2=1 - каноническое уравнение эллипса
полуоси 3 (вдоль оси х) и 1 (вдоль оси у)
F1 и F2 - фокусы эллипса, расположены на оси х, так как полуось вдоль х длиннее
фокусное расстояние с=корень(3^2-1^2)=2*корень(2)
F1=(-2*корень(2);0)
F2=(2*корень(2);0)
2)9x^2+25y^2-1=0
(x/(1/3))^2+(y/(1/5))^2=1 - каноническое уравнение эллипса
полуоси 1/3 (вдоль оси х) и 1/5 (вдоль оси у)
F1 и F2 - фокусы эллипса, расположены на оси х, так как полуось вдоль х длиннее
фокусное расстояние с=корень((1/3)^2-(1/5)^2)=4/15=0,2(6)
F1=(-4/15;0)
F2=(4/15;0)