Вариант для любителей тригонометрии
Объяснение:
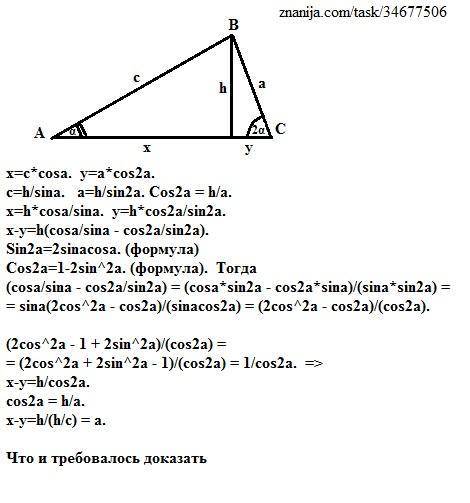
Дан треугольник АВС с основанием АС и высотой h, проведенной к основанию. Стороны треугольника
АВ = "с", ВС = "а".
Пусть основание делится высотой на отрезки, равные x и y, считая от вершины А. Тогда из прямоугольных треугольников, на которые высота делит исходный треугольник, имеем:
x = c*cosa. y = a*cos2a.
c = h/sina. a = h/sin2a. cos2a = h/а. =>
x = h*cosa/sina. y = h*cos2a/sin2a.
x - y = h(cosa/sina - cos2a/sin2a).
Sin2a = 2sina·cosa. (формула двойного аргумента)
Cos2a = 1 - 2sin²а. (формула двойного аргумента) Тогда
cosa/sina - cos2a/sin2a =
(cosa·sin2a - cos2a·sina)/(sina·sin2a). =>
sina(2cos²а - cos2a)/(sina·cos2a)=(2cos²а - cos2a)/(cos2a).
(2cos²а - 1 + 2sin²а)/(cos2a) =
(2cos²а + 2sin²а - 1)/(cos2a) = 1/cos2a. =>
x - y = h/cos2a. cos2a = h/а. =>
x - y = h/(h/а) = а.
Что и требовалось доказать.
Сумма односторонних углов равна 180 градусов
<1=100%
<2=100-20=80%
100+80=180 градусов
Сколько градусов составляют 1%
180:180=1
<1=1•100=100 градусов
<2=1•80=80 градусов
ИЛИ
180 градусов. - 180%
Х. - 100%
X=180•100:180=18000:180=100 градусов
180 градусов. - 180%
Х. - 80%
Х=180•80:180=14400:180=80 градусов
<1=100 градусов
<2=80 градусов
Объяснение: