По свойству биссектрисы, она равноудалена от сторон которые её образуют.
Значит биссектриса из угла A равноудалена от сторон AD и AB, а биссектриса из угла B равноудалена от сторон AB и BC => точка пересечения биссектрис(P) равноудалена от сторон AB,AD и BC значит она лежит на средней линии трапеции (MN).
Аналогично точка Q лежит на средней линии трапеции.
-----------------
Рассмотрим треугольник ABP, как известно сумма односторонних углов трапеции=180°, значит сумма их половинок=90°.
Значит ∠APB=180-90=90°.
Аналогично ∠DQC=90°.
Отрезки PM и QN - это медианы опущенные из прямых углов, они равны половине гипотенузы.
---------------------
Искомый отрезок 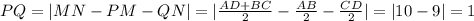
----------------------
ответ PQ=1
Решение
Объяснение:
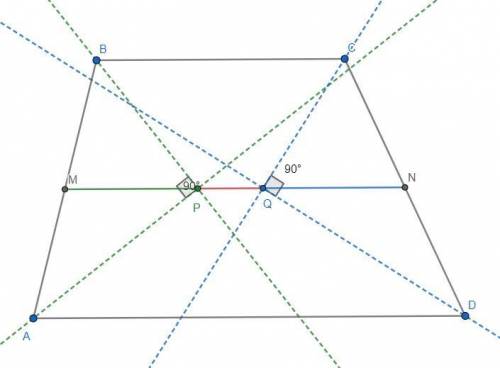
Радиус вписанной в равнобедренную трапецию окружности равен половине ее высоты.
Назовем трапецию ABCD (BC ║ AB), проведем высоту CK к точке K.
Вписанная окружность прикасается к серединам сторон.
Обозначим эти середины: M (AB), L (BC), N (CD), F (AD).
Касательные, проведенные с одной точки равны:
BM = BL = CL = CN = 2
AM = AF = DF = DN = 18
CD = 2 + 18 = 20
Рассмотрим ΔCKD:
∠CKD = 90° (CK - высота)
KD = (AD - BC) / 2 = (36 - 4) / 2 = 32/2 = 16 (по свойству равнобедренной трапеции)
KD = 16
По теореме Пифагора:
CK² = CD² - KD²
CK = √(400 - 256) = √144 = 12
CK = 12
r = CK/2 = 12/2 = 6
r = 6 см
Объяснение:
Расстояние от М до хорд АВ и АС - перпендикуляр, проведенный от М к этим хордам. От центра О окружности проводим перпендикуляр к хордам АВ и АС. Он делит хорды пополам.
ΔВН₁О прямоугольный ОВ=5 дм (радиус) ВН₁=АВ/2=3 дм, тогда по т. Пифагора ОН₁=√(5²-3²)=4 дм;
ΔОН₁М прямоугольный, ОМ=4 дм ОН₁=4 дм, по т. Пифагора:
Н₁М=√(4²+4²)=4√2 дм - расстояние от М до хорды АВ;
аналогично:
ΔВН₂О прямоугольный ОВ=5 дм (радиус) СН₂=АС/2=4 дм, тогда по т. Пифагора ОН₁=√(5²-4²)=3 дм;
ΔОН₂М прямоугольный, ОМ=4 дм ОН₂=3 дм, по т. Пифагора:
Н₂М=√(4²+3²)=5 дм - расстояние от М до хорды АС.