остроугольный и равнобедренный.
Объяснение:
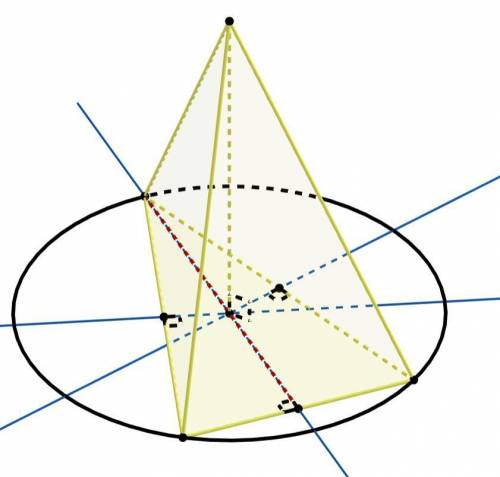
Если боковые рёбра пирамиды составляют равные углы с плоскостью основания, то основанием высоты пирамиды является центр окружности описанной около многоугольника из основания.
Центр окружности описанной около треугольника лежит внутри треугольника, если он остроугольный.
Так же этот центр лежит на пересечении серединных перпендикуляров к сторонам треугольника. Если центр описанной окружности лежит на одной высоте треугольника, то эта высота лежит на серединном перпендикуляре. А значит высота одновременно является и медианой. Тогда треугольник равнобедренный.
а) 80°. б) 70°.
Объяснение:
По данным условия и рисунка многогранние ABCF - треугольная пирамида.
а) Прямые АВ и В1С1 - скрещивающиеся по определению: "Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости и не имеют общих точек или другими словами это две прямые в пространстве, не имеющие общих точек, и не являющиеся параллельными".
Угол между скрещивающимися прямыми - это угол между любыми двумя пересекающимися прямыми, которые параллельны исходным скрещивающимся.
Так как В1С1 параллельна ВС, то угол между скрещивающимися прямыми АВ и В1С1 равен углу между пересекающимися прямыми АВ и ВС. То есть это угол АВС = 80° (дано).
б) Аналогично. Так как А1С1 параллельна АС, то угол между скрещивающимися прямыми А1С1 и ВС равен углу между пересекающимися прямыми АС и ВС. То есть это угол АСВ. В треугольнике АВС по сумме внутренних углов треугольника
∠АСВ = 180° - 30° - 80° = 70°.
Значит искомый угол равен 70°.