ответ: 5√3 см; 5√2 см
Объяснение:
у куба все ребра равны. квадрат диагонали куба равен сумме квадратов трех его измерений. значит, если ребро 5, то диагональ равна
√(5²+5²+5²)=√75=√(25*3)=5√3/см/
диагональ боковой грани - это диагональ квадрата со стороной 5см, она, как известно, равна √(5²+5²)=√50=5√2/см/
1) В четырехугольнике ABCD точки E и F — соответственно середины равных сторон AB и CD . Серединные перпендикуляр к стороне AD пересекает серединный перпендикуляр к стороне BC в точке P . Докажите, что серединный перпендикуляр, проведенный к отрезку EF проходит через точку P .
2) В четырехугольнике ABCD серединные перпендикуляры к сторонамAB и CD пересекаются на стороне AD . Известно, что \angle A = \angle D . Докажите, что в четырехугольнике диагонали равны.
3) В квадрате ABCD даны точки E и F соответственно на сторонах AB и BC ,причем \angle AED = \angle FED . Докажите равенство EF = AE + FC
так???!!!
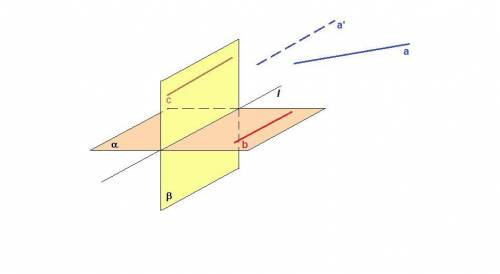
Предположим, что прямая а не пересекает плоскости α и β.
Значит, прямая а параллельна обеим плоскостям.
Тогда в каждой плоскости найдется прямая, параллельная прямой а. Пусть это прямые b и с.
Так как b║a и с║а, то b║c.
Если прямая с параллельна прямой b, лежащей в плоскости α, то с║α.
Плоскость β проходит через прямую с, параллельную плоскости α, и пересекает плоскость α, значит линия пересечения плоскостей параллельна прямой с.
Итак, c║l, c║a, ⇒ l║a. Но прямые l и а скрещивающиеся. Получили противоречие.
Значит, прямая а пересекает хотя бы одну из плоскостей.
5√3см
5√2см
Объяснение:
Диагональ куба находится по формуле:
D=a√3, где а- ребро куба.
D=5√3 см диагональ куба.
Диагональ квадрата находится по формуле:
d=a√2, где а -сторона квадрата (ребро куба)
d=a√2=5√2см