Боковые грани призмы - параллелограммы, и площадь каждого равна произведению высоты на основание.
Примем за основания граней (параллелограммов) боковые ребра. Они равны, а высоты - стороны треугольника в перпендикулярного сечения призмы, они разной длины.
Треугольник сечения подобен треугольнику со сторонами 9, 10, 17, площадь которого, найденная по ф.Герона, равна 36 (см²) (Можно без труда проверить)
Площади подобных фигур относятся, как квадрат коэффициента подобия их линейных элементов.
Если площадь сечения обозначить S, а площадь треугольника со сторонами 9,10,17 – S1, то S:S1=k²
S:S1=144:36=4
k²=3, ⇒k=√4=2
Следовательно, периметр сечения равен 2•(9+10+17)=72 см
Площадь боковой поверхности призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
S=72•8=576 см²
ответ:Номер 1
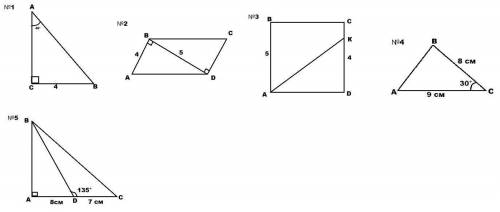
Если <А=45 градусов,а треугольник прямоугольный,то
<А=<В=45 градусов
Треугольник не только прямоугольный,но и равнобедренный,тогда
АС=СВ=4
Площадь треугольника-половина произведения высоты на основание
S=4•4:2=8 ед в квадрате
Номер 2
Площадь прямоугольного треугольника -половина произведения катетов
S=5•4:2=10 ед в квадрате
Номер 3
АК отсекла от квадрата трапецию
Ее основания
АВ=5
СК=5-4=1
СВ=5 Это высота
Площадь трапеции-произведение полусуммы оснований на высоту
S=(5+1):2•5=15 ед в квадрате
Номер 4
Провели высоту из точки В на основание АС,образовались два прямоугольных треугольника,у одного из них <С=30 градусов.В прямоугольном треугольнике катет,лежащий против угла 30 градусов,равен половине гипотенузы.В данном конкретном случае-гипотенуза ВС=8,а катет-высота,проведённая из точки В
Высота равна
8:2=4
S=9•4:2=18 ед в квадрате
Номер 5
<BDC+<ADB=180 градусов,как смежные углы
<АDB=180-135=45 градусов
Треугольник АВD прямоугольный,равнобедренный,углы при его основании равны по 45 градусов,а
АВ=АD=8
S=(8+7)•8:2=60 ед в квадрате
Объяснение: