Линейная зависимость векторов, линейная независимость векторов, базис векторови др. термины имеют не только геометрическую интерпретацию, но, прежде всего,алгебраический смысл. Само понятие «вектор» с точки зрения линейной алгебры – это далеко не всегда тот «обычный» вектор, который мы можем изобразить на плоскости или в пространстве. За доказательством далеко ходить не нужно, попробуйте нарисовать вектор пятимерного пространства . Или вектор погоды, за которым я только что сходил на Гисметео: – температура и атмосферное давление соответственно. Пример, конечно, некорректен с точки зрения свойств векторного пространства, но, тем не менее, никто не запрещает формализовать данные параметры вектором. Дыхание осени….
Нет, я не собираюсь грузить вас теорией, линейными векторными пространствами, задача состоит в том, чтобы понять определения и теоремы. Новые термины (линейная зависимость, независимость, линейная комбинация, базис и т.д.) приложимы ко всемвекторам с алгебраической точки зрения, но примеры будут даны геометрические. Таким образом, всё просто, доступно и наглядно. Помимо задач аналитической геометрии мы рассмотрим и некоторые типовые задания алгебры. Для освоения материала желательно ознакомиться с уроками
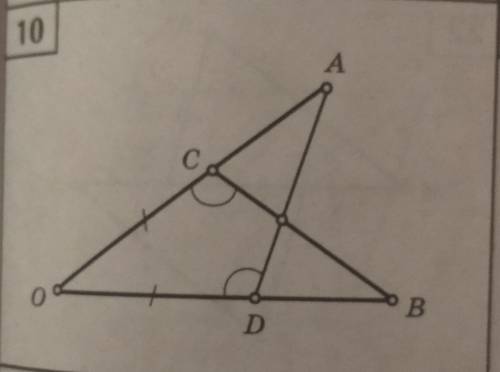
-Рисунок смотрите в приложении-
Дано:
Прямые а и b.
с и m - секущие.
∠1 = ∠2 = 45°.
∠3 = 60°.
Найти:
∠4 = ?
Рассмотрим ∠1 и ∠2 - соответственные. Так как они имеют одинаковую градусную меру, то они равны. При пересечении двух прямых a и b секущей c соответственные ∠1 = ∠2, то прямые а║b (по признаку параллельности прямых).Рассмотрим ∠3 и ∠5 - односторонние, образованные пересечением параллельных прямых а и b секущей m. Поэтому, ∠3+∠5 = 180° (свойство односторонних углов при параллельных прямых). Отсюда, ∠5 = 180°-∠3 = 180°-60° = 120°.∠5 и ∠4 - вертикальные, поэтому ∠5 = ∠4 = 120°.ответ: 120°.