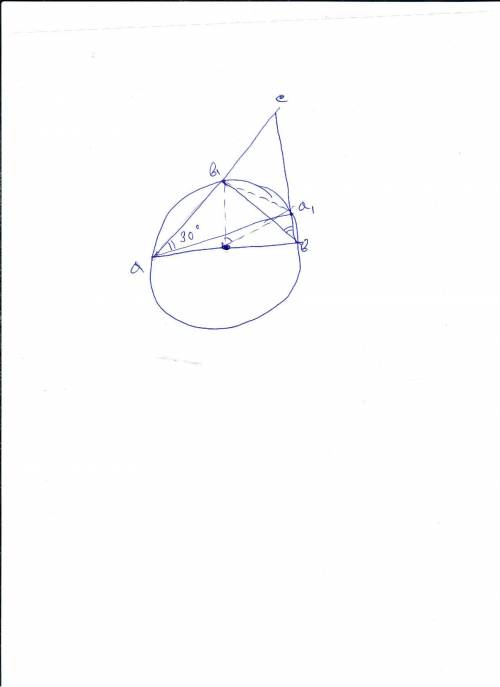
Условия не достаточно. Вокруг а1b1ab можно описать окружность у которой ab -диаметр. Отрезок а1b1-равен радиусу. Угол a1bb1 равен 30 градусам (половина центрального угла). Если угол abc=сab, то abc равен 60.
Значит угол abc - любой из диапазона (30, 90) градусов.
Угол стремится к 90, когда второй угол стремится к 30, т.е. треугольник становится прямоугольным, а b1a1 его высота к гипотенузе (точки b и b1 совпадают и b1a1 равен ba/2)
Вот если треугольник не просто острый, а равнобедренный, то abc=60 градусам.
Условия не достаточно. Вокруг а1b1ab можно описать окружность у которой ab -диаметр. Отрезок а1b1-равен радиусу. Угол a1bb1 равен 30 градусам (половина центрального угла). Если угол abc=сab, то abc равен 60.
Значит угол abc - любой из диапазона (30, 90) градусов.
Угол стремится к 90, когда второй угол стремится к 30, т.е. треугольник становится прямоугольным, а b1a1 его высота к гипотенузе (точки b и b1 совпадают и b1a1 равен ba/2)
Вот если треугольник не просто острый, а равнобедренный, то abc=60 градусам.

АА1 = 6 см.
Объяснение:
АА1║ВВ1║СС1 => Прямые АВ, АА1, ВВ1 и СС1 лежат в одной плоскости, которая пересекает плоскость α по прямой А1В1.
Пусть точка О - точка пересечения отрезка АВ и плоскости альфа. Треугольники ВОВ1 и СОС1 подобны, так как ВВ1║СС1. Из подобия имеем: ВВ1/СС1 = 10/4 = 5/2. =>
ОС = (2/5)·ВО.
ВС = ВО - (2/5)·ВО = (3/5)·ВО.
АО = АС - ОС. АС = (5/3)·ВС (дано). =>
АС = (5/3)·(3/5)·ВО = ВО.
АО = ВО - ОС = ВО - (2/5)·ВО = (3/5)·ВО.
Треугольники АОА1 и ВОВ1 подобны, так как АА1║ВВ1. =>
АА1/ВВ1 = АО/ВО = 3/5. =>
АА1 = (3/5)·ВВ1 = (3/5)·10 = 6 см.