Допустим, могут.
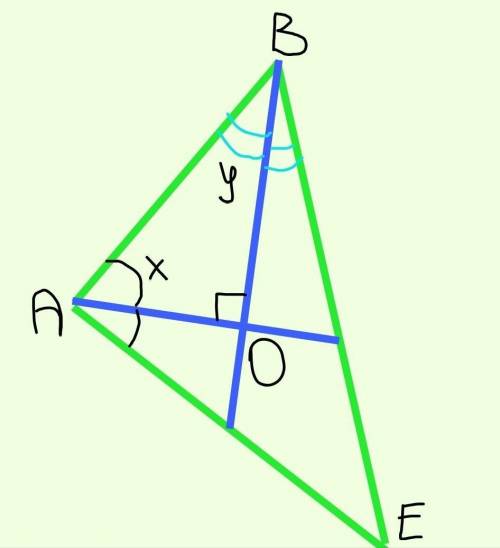
Тогда угол АОВ=90°.
Пусть угол ВАО=х, а угол АВО=у.
Сумма острых углов в прямоугольном треугольнике равна 90°. Тоесть угол ВАО+угол АВО=90°;
х+у=90
2(х+у)=90*2
2х+2у=180
Так как АО и ВО – биссектрисы углов ЕАВ и АВЕ соответственно, то угол ЕАО=угол ВАО=х; угол ОВЕ=угол АВО=у.
Из найденного: х+у=90 => 2х+2у=180
2х+2у=угол ЕАО+угол ВАО+угол ОВЕ+угол АВО
2х+2у=угол ЕАВ+угол АВЕ
=> Угол ЕАВ+угол АВЕ=180°
Сумма углов в любом треугольнике равна 180°.
Следовательно угол АЕВ=180°–(угол ЕАВ+угол АВЕ)=180°–180°=0°.
Величина угла выражается положительным числом, значит 0 она быть не может.
Получим что биссектрисы не могут пересекаться под прямым углом.
Получим что биссектрисы не могут пересекаться под прямым углом.ответ: Нет.
Объяснение:
1а) в приложенном файле.
1б)ΔKMN-прямоугольный , по свойству угла 30°⇒ KN=0,5*36=18.
Пусть NP=х , тогда РМ=36-х. Катет в прямоугольном треугольнике есть среднее пропорциональное между проекцией и гипотенузой : KN=NP*NM или 18²=х*36 , х=9, NP=9 , РМ=36-9=27
2б)
1)ΔСЕD=ΔCFD как прямоугольные по катетам ЕD=DF и гипотенузе CD-общая. В равных треугольниках соответственные элементы равны :∠ЕCD=∠FСD и СЕ=СF.
2)∠АЕD=∠ВFD=90.
ΔАЕD=ΔВFD как прямоугольные по катетам ЕD=DF и гипотенузам АD=DВ . В равных треугольниках соответственные элементы равны : АЕ=ВF и ∠А=∠В.
3) Т.к АЕ=ВF и
СЕ=СF , то АС=ВС.
ΔАСD=ΔВСD по стороне и двум прилежащим углам : АС=ВС, ∠ЕCD=∠FСD, ∠А=∠В.
2а) в приложенном файле.
2б)ΔKMN-прямоугольный , по свойству угла 30°⇒ KN=0,5*36=18.
Пусть NP=х , тогда РМ=36-х. Катет в прямоугольном треугольнике есть среднее пропорциональное между проекцией и гипотенузой : KN=NP*NM или 18²=х*36 , х=9, NP=9 , РМ=36-9=27