Пусть АВСД четырёхугольник, вписанный в окружность,
<A : < B : < C = 2 : 6 : 7. Примем часть за х. То есть
<A = 2 * х; < B = 6 * х; < C = 7 * х.
Как известно в четырёхугольнике, вписанном в окружность сумма противоположных углов равна 180°, то есть <A + < C = 180°, <B + <Д = 180°.
<A + < C = 2 * х + 7 * х = 9 * х = 180°. х = 180°/9 = 20°.
<A = 2 * х = 2 * 20° = 40°;
< B = 6 * х = 6 * 20° = 120°;
< C = 7 * х = 7 * 20° = 140°;
< Д = 180° - < В = 180° - 120° = 60°.
ответ: 10 см.
Объяснение:
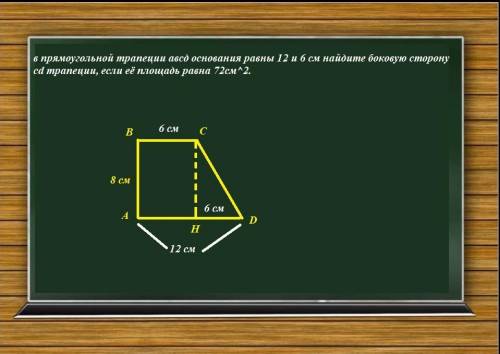
в прямоугольной трапеции авсд основания равны 12 и 6 см найдите боковую сторону сd трапеции, если её площадь равна 72см^2.
Решение
S=h(a+b)/2, где S=72 см^2 площадь трапеции; а=12 см - нижнее основание, b=6 см - верхнее основание: h - высота в см.
h(12+6)/2=72;
18h/2=72;
9h=72;
h=72:9;
h=8 см - высота трапеции.
Проведем высоту СН трапеции.
(См. скриншот).
В полученном треугольнике CDH CH=8 см; DH=12-6=6 см. Тогда по т. Пифагора
CD²=СH²+DH²=8²+6²=64+36=100;
CD=√100=10 см.
Объяснение:
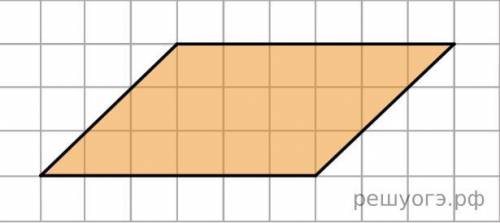
S=a×h
a - сторона
h- высота
S=6×3=18 (ед^2)