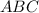 , и точки
, и точки 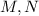 на стороне
на стороне 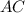 , и точки
, и точки 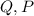 на сторонах
на сторонах 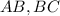 соответственно .
соответственно . 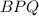 и
и 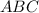 подобны друг другу. Так как
подобны друг другу. Так как  , выведем некие следствия из подобия:
, выведем некие следствия из подобия: 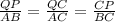 , или же это соотношение можно записать так , выражая отрезки
, или же это соотношение можно записать так , выражая отрезки 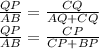
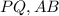 по теореме косинусов
по теореме косинусов 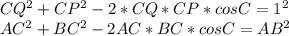
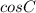 и приравнивая получим:
и приравнивая получим: 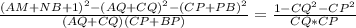
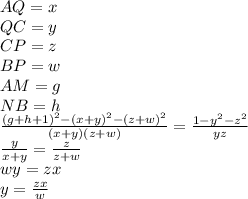
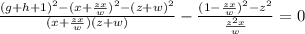
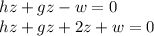
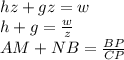 в дальнейшем это соотношение понадобится
в дальнейшем это соотношение понадобится 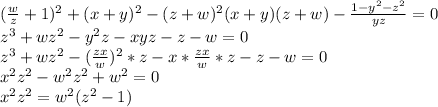
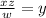 тогда
тогда 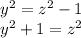 то есть треугольник выходит прямоугольный при наличии именно определенного соотношения! Тогда
то есть треугольник выходит прямоугольный при наличии именно определенного соотношения! Тогда 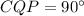 тогда и
тогда и 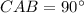
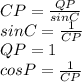
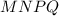 будет сторона
будет сторона 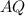 , а так как площадь параллелограмма равна основание на высоту опущенную на нее, то площадь параллелограмма равна
, а так как площадь параллелограмма равна основание на высоту опущенную на нее, то площадь параллелограмма равна 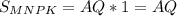 , и она равна
, и она равна 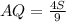
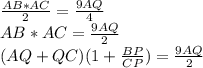 , но так как
, но так как 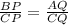 то
то 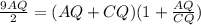 с него следует
с него следует 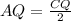 . Тогда
. Тогда 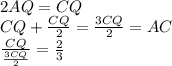 , то есть коэффициент подобия равен
, то есть коэффициент подобия равен 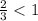 верно ! тогда
верно ! тогда 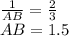
Дано:
тр АВС (уг С=90)
АС = 16 см
ВС = 12 см
АВ = 20 см
Найти:
а) косинус меньшего угла
б) сумму квадратов косинусов острых углов
а) по свойству соотношения сторон и углов треугольника, против меньшей стороны лежит меньший угол, а значит меньшим будет угол, лежащий против стороны 12 см, по условию, следовательно, это угол А.
cos A = AC / AB; cos A = 4/5 = 0.8
б) Есть св-во - оно же основное геометрическое тождество, сумма квадратов косинусов острых углов прямоугольного треугольника равна единице, но вы похоже этого ещё не изучали, посему надо найти оставшийся косинус угла В и найти сумму квадратов косинусов вычислением, приступим:
cos B = CB / AB; cos B = 12/20 = 3/5 = 0.6
cos²A +cos²B = 0.8²+0.6²=0.64+0.36=1