
1:2=0,5
9+12=21
0,5(21)=10,5
10,5×6=63
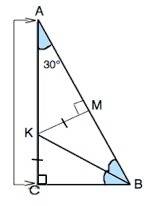
Обозначим данный треугольник АВС, ∠С=90°, ∠А=30°, ВК- биссектриса ∠АВС, КМ⊥АВ.
Сумма острых углов прямоугольного треугольника равна 90°.
∠САВ=30°, ∠АВС=60°.
Биссектриса делит угол пополам, ⇒∠КВС=∠КВМ=30°
Прямоугольные ∆ КВС=∆ КВМ по острому углу и общей гипотенузу. ⇒
КС=КМ.
В ∆ АКМ катет КМ противолежит углу 30° и равен половине гипотенузы АК (свойство).
Примем КМ=а
Тогда АК=2а
Так как КС=КМ, то АС=3а
3а=18, а=6 см.
КС=а=6 см, КА=18-6=12 см
* * *
Решить задачу можно разными Например, по т. Пифагора найти АВ и ВС и применить и свойство биссектрисы, которая делит противоположную углу сторону в отношении прилежащих сторон. Можно воспользоваться функциями острых углов, - это зависит от темы, которую в настоящее время проходите, но данное решение самое простое.
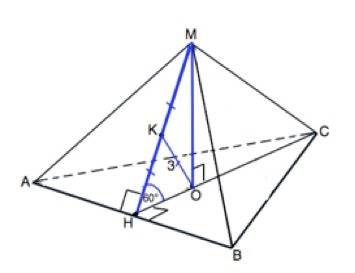
В правильной треугольной пирамиде двугранный угол при основании равен 60°. Отрезок, соединяющий основание высоты пирамиды с серединой апофемы, равен 3. Найдите площадь полной поверхности пирамиды.
* * *
Решение.
Двугранный угол измеряется величиной линейного угла между двумя лучами, проведенными перпендикулярно к одной точке ребра двугранного угла.
Боковая грань правильной пирамиды - равнобедренный треугольник. Апофема МН и высота СН основания перпендикулярны ребру АВ в его середине Н. АН=ВН.
Угол МНС - линейный угол двугранного угла при основании пирамиды.
Вершина правильной пирамиды проецируется в центр основания - точку пересечения его медиан ( высот, биссектрис).
Высота пирамиды МО - перпендикулярна плоскости основания,⇒
МО⊥СН.
∆ МОН - прямоугольный, КО - его медиана.
По свойству медианы прямоугольного треугольника МК=КН=КО=3, ⇒ МН=2•3=6
По условию ∠КНО=60°.
В ∆ КОН стороны КО=НК ⇒ НО=КО=3
СН медиана и высота основания АВС,
Медианы треугольника точкой их пересечения делятся в отношении 2:1, считая от вершины.
СН=3•ОН=9.
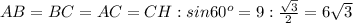
S ∆ ABC=CH•AB:2=0•6√3:2=27√3
S бок=3•МН•AB:2=3•6•6√3:2=54√3
Sполн=27√3+54√3=81√3 (ед. площади)
Мне тоже надо кто не будь