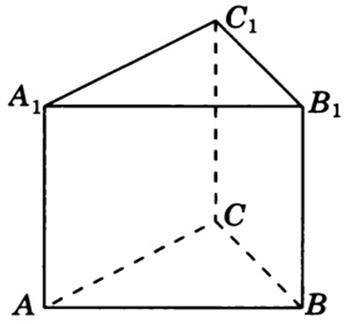
Нехай задана правильна трикутна призма, бічні грані якої є квадратами, а 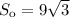 см² — площа основи цієї призми.
см² — площа основи цієї призми.
Основа призми є правильним (рівностороннім) трикутником зі строною  см. Знайдемо цю сторону, скориставшись площею рівностороннього трикутника:
см. Знайдемо цю сторону, скориставшись площею рівностороннього трикутника: 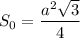
Отже, 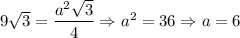 см.
см.
Через те що бічні грані є квадратами, тоді ребра призми дорівнюють 6 см (за властивістю квадрата) — ребра правильної призми є висотою призми.
Об'єм правильної трикутної призми можна розрахувати за формулою
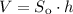 , де
, де 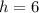 см — висота призми.
см — висота призми.
Знайдено значення шуканої величини:
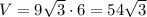 см³
см³
Відповідь: А) 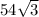 см³
см³
тут всё очевидно же
Объяснение:
Средняя линия треугольника и её свойства. Определение: средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. У средней линии есть два свойства : первое свойство: средняя линия треугольника параллельна основанию и второе свойство: средняя линия равна половине основания. Доказательство. Через середину E боковой стороны BC проведём прямую ED параллельно основанию AC. По теореме Фалеса другая боковая сторона тоже разделится пополам. Значит, D — середина стороны AB, то есть отрезок ED — это средняя линия. А по построению наш отрезок параллелен основанию, вот и доказана параллельность средней линии основанию. Теперь докажем второе свойство: через точку D проведём прямую DF, параллельную боковой стороне BC. По теореме Фалеса основание AC разделится пополам, то есть точка F — середина стороны AC, и FC равно половине основания. А многоугольник CEDF — это параллелограмм (по построению), его противоположные стороны равны, то есть отрезок DE равен половинке основания — отрезку FC. То есть средняя линия равна половине основания. ЧТД.