Объяснение:
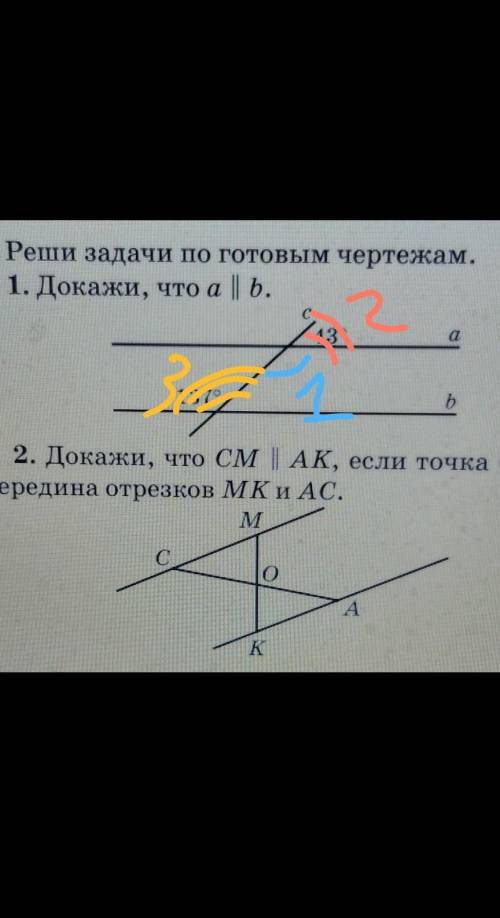
#1
Угол 1 и угол 2 смежные. Сумма смежных углов равна 180 градусов => 180-43=137°-угол
Угол 3=углу 1 => угол 1 и угол 3-накрест.леж=> а||б по признаку накрест.леж углов
#2
Рассмотрим треугольники СОМ и КОА
1. Угол СОМ=углу КОА, тк вертикальные
2. МО=ОК, тк т.О середина отрезка МК
3. СО=ОА, тк т.О середина отрезка АС => треугольник СОМ=треугольнику КОА по двум сторонам и углу между ними
В равных треугольниках соответствующие элементы равны => угол КАО=углу ОСМ
Угол КАО и угол ОСМ -накрест.леж=> СМ||АК по признаку накрест.леж углов
равнобедренный ΔАОС (О - центр основания конуса): АО=ОС=R, <AOC=120°, <OAC=<OCA=30°, OM_|_AC, ОМ - высота, медиана ΔАОС, ⇒АМ=3√3.
tg30°=OM:AM.
по условию, секущая плоскость составляет с плоскостью основания угол 45°, ⇒ линейный угол ВАСМ - угол ВМО=45°. высота конуса Н=ОМ=3
ответ: Vк=20,25π
2. MABCD - правильная пирамида с диагональю основания АС=d, угол между боковым ребром МА и плоскостью основания <MAC= α
MO_|_(MABCD), МО - высота пирамиды.
прямоугольный ΔМОА: ОА=d/2, <A=α. tgα=MO:OA, MO=tgα*OA
MO=d*tgα/2
Vпир=(1/3)*Sосн*H
Sосн=a², a- сторона основания пирамиды
диагональ пирамиды найдена по теореме Пифагора из ΔАВС: АС²=АВ²+АС²
АВ=АС=а
d²=a²+a², d²=2a². d=a√2, ⇒a=d/√2
S=(d/√2)²=d²/2
Vпир=(1/3)*(d²/2)*(d*tgα/2)
Vпир=(d³ *tgα)/12