Две прямые лежат в одной плоскости, если смешанное произведение их направляющих векторов и третьего вектора, проведённого между двумя точками, лежащими на этих прямых, равно 0 . (При равенстве нулю смешанного произведения делаем вывод о компланарности трёх векторов.)
Из уравнения прямых можно выписать координаты направляющих векторов и координаты точек, лежащих на прямых .
\begin{gathered}l_1:\; \frac{x-1}{2}=\frac{y+2}{-1}=\frac{z}{-2}\; \; ,\; \; \vec{s}_1=(2,-1,-2)\; ,\; \; M_1(1,-2,0) l_2:\; \frac{x+1}{1}=\frac{y+11}{2}=\frac{z+6}{1}\; \; ,\; \; \vec{s}_2=(1,2,1 )\; \; ,\; \; M_2(-1,-11,-6)overline {M_2M_1}=(1+1,-2+11,0+6)=(2,9,6)(\overline {M_2M_1},\vec{s}_1,\vec{s}_2)= \left|\begin{array}{ccc}2&9&6\\2&-1&-2\\1&2&1\end{array}\right|= 2(-1+2)-9(2+2)+6(4+1)=0\end{gathered}
l
1
:
2
x−1
=
−1
y+2
=
−2
z
,
s
1
=(2,−1,−2),M
1
(1,−2,0)
l
2
:
1
x+1
=
2
y+11
=
1
z+6
,
s
2
=(1,2,1),M
2
(−1,−11,−6)
M
2
M
1
=(1+1,−2+11,0+6)=(2,9,6)
(
M
2
M
1
,
s
1
,
s
2
)=
∣
∣
∣
∣
∣
∣
∣
2
2
1
9
−1
2
6
−2
1
∣
∣
∣
∣
∣
∣
∣
=2(−1+2)−9(2+2)+6(4+1)=0
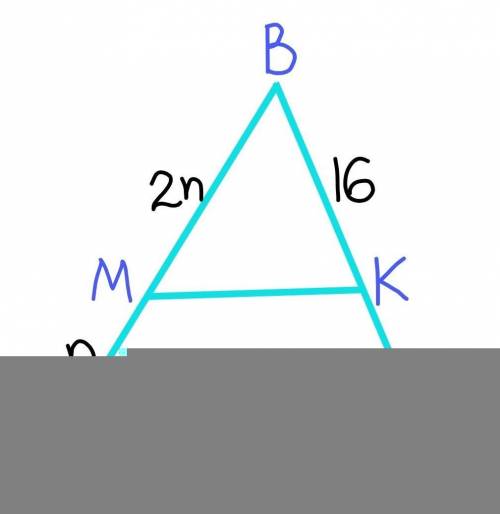
№1
Так как МК//АС по условию, то угол BMK=угол ВАС как соответственные при параллельных прямых МК и АС и секущей АВ.
Угол АВС – общий.
Тогда ∆МВК~∆АВС по двум углам.
Стороны подобных треугольников пропорциональны, то есть:
МВ/АВ=ВК/ВС
МВ/(АМ+ВМ)=ВК/BC
Пусть АС=n, тогда МВ=2n
2n/(n+2n)=16/BC
2n/3n=16/BC
2/3=16/BC
16*3=2*BC
48=2*BC
BC=24 см
ответ: 24 см.
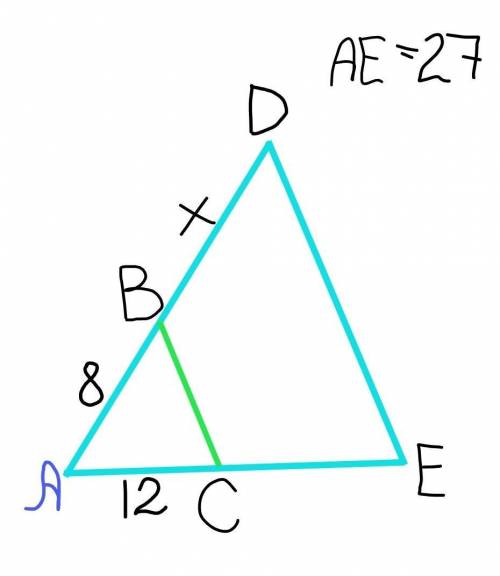
№2
Так как ВС//DE по условию, то угол АСВ=угол АЕD как соответственные при параллельных прямых ВС и DE и секущей АЕ.
Угол DAE – общий.
Тогда ∆АСВ~∆АЕD по двум углам.
Стороны подобных треугольников пропорциональны, то есть:
АВ/АС=АD/AE
8/12=AD/27
2/3=AD/27
3*AD=27*2
3*AD=54
AD=18 см
ВD=AD–AB=18–8=10 см
ответ: 10 см
радиус круга равен половине стороны квадрата, т.к. круг вписан в него,
радиус равен двум,
отношение биссиктрисс в точке разрыва относится как два к одному от вершины ( есть такое свойство), отсюда две части равно двум см, следоаательно три части трем см, далее рассмотрим прямоугольный треуг. у которого катет один равен трем, углы равны 60° и 30°, по свойству каьета лежащего против угла в 30° он равен половине гиппоьинузы, пусть этот катет равен х, тогда гипп равна 2х
из т.П. 3=√(4х^2-х^2)=х√3=> х=3/√3=√3, отсюда гипп равна 2√3
и найдем площадь треугольника
sΔ=1/2 *3*2√3=3√3 см^2