Пусть нам известна хотя бы сторона этого шестиугольника:))). Пусть она равна а. Кстати, радиус описанной окружности тоже равен а. Этот шестиугольник состоит из 6 равных треугольников. Достаточно вычислить площадь хотя бы одного. Треугольники будут равносторонними. потому что угол при вершине треугольника, где центр этого шестиугольника, равен 360:6=60. А другие два угла равны между собой как в равнобедренном треугольнике. Значит 180-60=120 градусов - сумма двух одинаковых углов треугольника. 120:2=60 градусов - мера углов при основании треугольника. Площадь равностороннего треугольника со стороной а можно вычислить по формуле, перемножив две одинаковые стороны друг на друга, затем умножив на синус 60 градусов и разделить пополам.
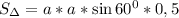
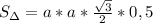
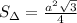
Всего таких треугольников 6. Значит надо умножить на 6.
Получается ответ
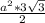
А как вам такое решениеце? Высота к гипотенузе делит прямоугольный треугольник на два, ему же подобных (и подобных между собой, конечно) Поскольку в этих треугольниках оба катета исходного треугольника играют роль гипотенузы, площади этих треугольников отностятся как квадраты катетов (в данном случае - соответственных сторон)
S1/S2 = (6/8)^2 = 9/16;
В сумме S1 + S2 = 8*6/2 = 24;
Остюда очень легко найти S1, S2 и их разность :)
Вот один из Пусть S1 = 9x; S2 = 16x, где х - неизвестная величина.
Тогда S1 + S2 = 25x = 24; x = 24/25;
S2 - S1 = (16 - 9)*x = 7*24/25 = 6,72;
ответ:64
Объяснение:
Дано:
ABCD - прямоугольник;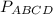 =40.
=40.
Найти: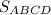
P=AB+CD+BC+AD
AD:CD=1:4 (по усл.)
AB=CD (по св-ву прямоуг.)
BC=AD (по св-ву прямоуг.)
Пусть DC=4x, AD=x.
Составим ур-е:
P=x+x+4x+4x
40=x+x+4x+4x
40=10x
x=4
DC=4·4=16
S=DC·AD
S=16·4=64