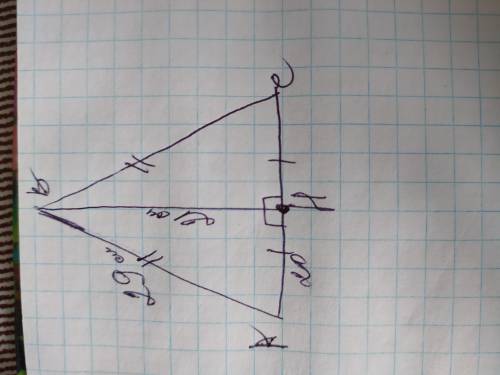
Обозначим этот треугольник АВС, с вершиной В, основанием АС и высотой ВН. Высота ВН делит ∆АВС на 2 одинаковых прямоугольных треугольников АВН и ВСН, так как треугольник равнобедренный; также ВН является в равнобедренном треугольнике ещё и медианой, поэтому высота ВН делит АС пополам и АН=НС. Рассмотрим один из них, к примеру ∆АВН. Боковая сторона АВ является в нём гипотенузой, а высота ВН - катетом. Найдём по теореме Пифагора катет АН. АН=29²-21²=√(841-441)=√400=20см
АН=НС=20см, тогда АС=20×2=40см
Основание АС=40см.
Теперь найдём площадь ∆АВС по формуле: ½ ×a×h, где h- высота, "а"- сторона, к которой проведена высота:
S= ½ × 40×21=420см²; S=420см²
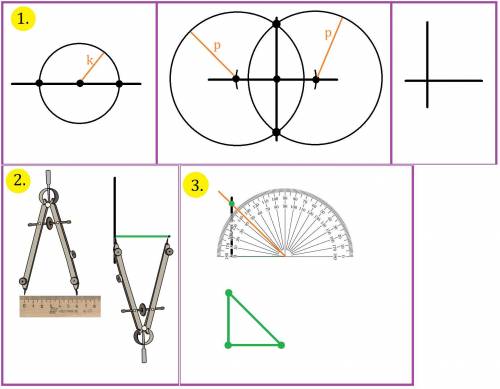
Проведём 2 перпендикулярные прямые (см. рис. 1). Для этого:
1. Из точки на произвольной прямой, проведём окружность произвольного радиуса k.
2. В точках пересечения окружности с прямой, проведём окружности с радиусом p, при это p > k.
3. Через точки пересечений окружностей проводим прямую, она будет перпендикулярна первой прямой.
С циркуля замерим на линейке 6 см и отложим 6 см на одной стороне прямого угла (см. рис. 2).
С транспортира отложим угол в 45° и соединим точки, как показано на рис. 3. Получили искомый треугольник.
120°; 120°; 120°
Объяснение:
В равностороннем треугольнике все углы по 60°.
Все углы треугольника являются вписанными, тогда центральные углы в два раза вписанного
60°- вписанный угол.
Дуга=60°*2=120°