на фотографии
Объяснение:
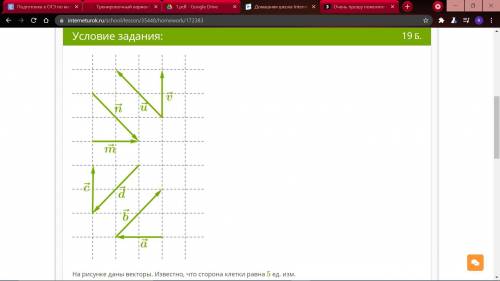
1) y = cosx - косинусоида
2) y=cosx - 1. Смещение по оси Оy на 1 вниз, то есть, середина будет косинусоиды будет на -1
3) y = cos (x+п/3). Смещение по оси Ox влево на п/3, то есть график будет начинается с п/3
4) y = 6cosx. Так как это тригонометрическая функция, то растягиваться график будет по оси Oy в 6 раз.
Лучше всего сначала наметить точки "нового" начала. Координата будет (-п/3; -1), а потом строить относительно этого "начала" график функции y=cos x.
Так как -п/3 = -60 градусов, то мы постоянно прибавляем 90 градусов, а потом впоследствии переводим в радианы, строя постепенно косинусоиду. Например -60 гр. + 90 гр. = 30 градусов. Следовательно: 30 x п/180 = п/6. Применяем формулу перевода из градусы в радианы угол (радианы) = угол (градусы) x п/180
Получится громоздкая косинусоида, которая смещена в 3 четверти координатной плоскости, то есть в четверти координатной плоскости, где и по иксу, и по игреку значения отрицательные.
Сделаем рисунок.
Стороны равнобедренного треугольника суть: АВ = BC=50 см и AС= 60 см. Проведены высоты АЕ и CD, и точки D и Е соединены. Определить стороны треугольника DBE.
Решение:
Вычислим площадь треугольника по формуле Герона.
S=√p (p−a) (p−b) (p−c)
(Нет нужды приводить здесь вычисления, они не влияют на ход и решения)
S Δ АВС=1200 см²
Найдем длину высоты АЕ к боковой стороне
АЕ =2·1200:50=48
По теореме Пифагора найдем длину боковых сторон меньшего треугольника.
ВЕ²=DB²=ВС²-АЕ²=196
ВЕ=14 см
Треугольники BDE и АВС подобны.
Угол В - общий, углы при основании равны как углы при параллельных прямых и секущей.
Найдем коэффициент k подобия треугольников BDE и АВС
k=14:50=0,28
DE=AC·0,28=16,8 см
ответ:
Стороны равны 14 см,14 см, 16,8 см