Question

Впрямоугольной системе координат даны векторы а(3; -2) и b(1; -2).найдите координаты вектора с=5a-9b и его длинну.постройте вектор с,если его конец совпадает с точкой m(3; 2)

Answer 1

Итак, мы имеем вектор a{3;-2} и вектор b{1;-2}.
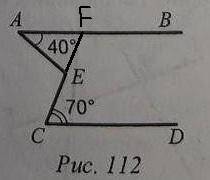
Умножение вектора на число: p*a=(pXa;pYa;), где p - любое число.
В нашем случае имеем: вектор 5а{15;-10} и вектор 9b{9;-18}.
Разность векторов : a-b=(Xa-Xb;Ya-Yb).
В нашем случае имеем: вектор c=5а-9b={15-9;-10-(-18)}={6;8}.
Итак, мы имеем вектор с{6;8}.
Модуль или длина вектора: |c|=√(Xc²+Yc²) или |с|=√(36+64)=10.
Координаты вектора ab равны разности соответствующих координат точек его конца и начала ab{x2-x1;y2-y1).
В нашем случае координаты вектора с известны: Xc=6 и Yc=8. Известны и координаты его конца: Xm=3 и Ym=2.Пусть точка N - начало вектора с. Зная, что Xc=Xm-Xn и Yc=Ym-Yn, находим координаты начала вектора с (точки N). Эти координаты будут: Xn=Xm-Xc или Xn=3-6=-3 и Yn=Ym-Yc или Yn=2-8=-6.
Остается только на координатной плоскости отметить две точки: N(-3;-6) и M(3;2).
Соединив эти две точки, получим искомый вектор С.