Картинка в этой задаче действительно желательна.
Объем правильной треугольной призмы равен произведению площади основания на высоту призмы.
Площадь основания - это площадь правильного треугольника со стороной а.
Формула площади равностороннего треугольника
S=(a²√3):4
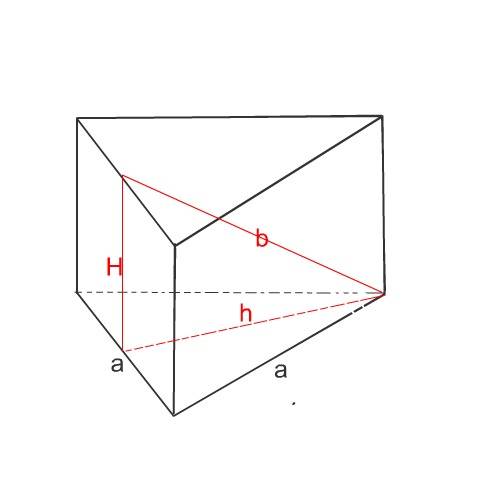
Высоту призмы найдем из прямоугольного треугольника,
катеты в котором- высота призмы и высота треугольника=основания,
а гипотенуза - данное в условии расстояние b от вершины одного основания до противолежащей стороны другого основания.
Высота правильного треугольника находится по формуле
h=а√3):2
Высоту призмы найдем по теореме Пифагора:
Н= √(b²-h²)=√(b²-3а²:4)
V= (a²√3):4)·√(b²-3а²:4)
Высота МТ треугольника КМР является биссектрисой этого треугольника. Докажите, что данный треугольник является равнобедренным.
Доказательство. Рассмотрим треугольники КМТ и РМТ . Их элементы - углы КТМ и РТМ равны 90 град (МТ - высота по условию), и углы КМТ и РМТ равны (т.к. МТ - биссектриса по условию), и МТ общая сторона. Воспользуемся равенством треугольников по стороне и двум прилежащим углам, откуда треугольник КМТ = РМТ. Следовательно,все элементы в них равны, тогда КМ=РМ. Значит, треугольник КМР является равнобедренным.
Удачи ! )