

Объяснение:
y = ax 2 + bx + c ( a , b , c — числа , a ≠ 0)
с областью определения — множеством R всех действительных чисел.
Функция y = x2 является частным случаем квадратичной функции y = ax2 + bx + c при a = 1, b = 0, c = 0.
График квадратичной функции (как и график функции y = x2) называется параболой , а уравнение y = ax2 + bx + c (a ≠ 0) — уравнением этой параболы.
Стр. 221
График квадратичной функции и его свойства мы будем изучать, используя свойства графика функции y = x2.
При а ≠ 1, b = 0, c = 0 имеем еще один частный случай квадратичной функции y = ax2 + bx + c, т. е. функцию
y = ax2 (a ≠ 0, a ≠ 1).
Пусть a > 0. Приведем два примера функции y = ax2:
1) при a > 1; 2) при 0 < a < 1.
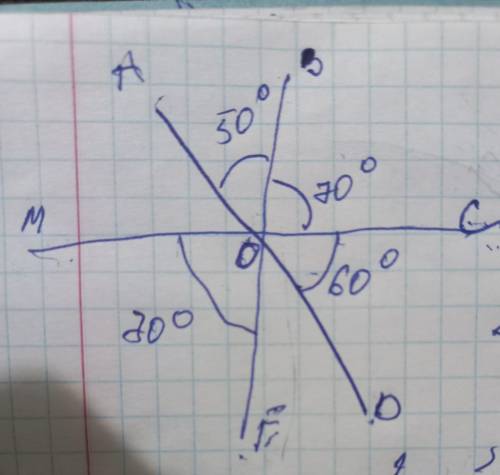
<АОС=<АОВ+<ВОС
<АОС=50°+70°=120°
<ВОD=<BOC+<COD
<BOD=70°+60°=130°
<MOC=180° ( потому что развёрнутый )
<FOD=<MOC-<MOF-<COD
<FOD=180°-70°-60°=50°
<COF=<COD+<FOD
<COF=60°+50°=110°