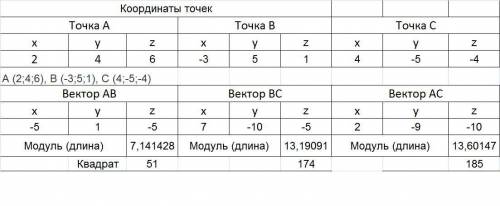
Находим координаты векторов и модули (вложение 1).
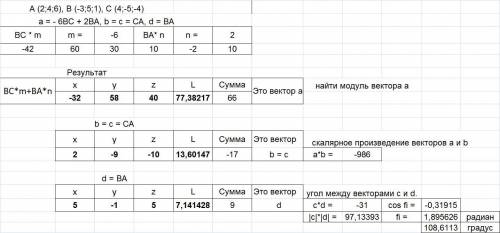
Находим модуль вектора а, скалярное произведение векторов а и b, угол между векторами c и d (вложение 2).
Приводим более подробное решение по определению угла меду векторами c и d (пусть они записаны как a и b).
Найдем скалярное произведение векторов:
a · b = ax · bx + ay · by + az · bz = 2 · 5 + (-9) · (-1) + (-10) · 5 = 10 + 9 - 50 = -31 .
Найдем длины векторов:
|a| = √ax2 + ay2 + az2 = √22 + (-9)2 + (-10)2 = √4 + 81 + 100 = √185 .
|b| = √bx2 + by2 + bz2 = √52 + (-1)2 + 52 = √25 + 1 + 25 = √51 .
Найдем угол между векторами:
cos α = (a · b ) / |a||b| .
cos α = -31 / (√185*√51) =
= - 31/√9435 = -31*√9435 / 9435 ≈ -0.319146.
Так как точка М по условию находится на равном расстоянии от А и В, она должна лежать на биссектрисе угла С
( которая для этого треугольника и медиана, и высота, хотя для решения данной задачи важна лишь биссектриса).
Соединим точку М с вершинами А и В.
Опустим из М перпендикуляр МН на АС.
МН в прямоугольном треугольнике противолежит углу 30° и потому равна половине гипотенузы СМ.
МН=1/2
АС - сторона равностороннего треугольника - равна АН+НС
АН найдем по т. Пифагора из треугольника АМН
АН=√(4 -1/4)=(√15):2
СН=СМ*cos(30°)=(√3):2
Сложим АН и СН и получим
АС=√3(√5+1):2
Площадь равностороннего треугольника равна квадрату его стороны, умноженному на корень из трех и деленному на 4.
S={√3(√5+1):2}²(√3):4
S={3(6+2√5)(√3):16=(18√3+6√15):16=
=(9√3+3√15):8
ответ:(9√3+3√15):8 ( трудно назвать ответ изящным, но он верный).
Если извлечь корни, то
S≈3,4 см².
Рисунок к задаче очень простой, его несложно сделать самостоятельно.( какой-то сбой - не загружается)