
Построим координатный параллелепипед точки А. Отметим на оси х — Ах(1;0;0); у — Ау(0;2;0); z — Аz (0;0;3).
Затем из точки Ах проведем две прямые, параллельную оси у и оси z, из точки Ау — прямые параллельные оси x и оси z; из Аz — параллельные оси х и оси у.
При пересечении прямых получаются точки Аху, Ауz, Ахz. Тогда
AxAxy = 2; AxAxz = 3; AyAxy = 1; AyAyz = 3; AzAxz = 1; AzAyz = 2;
Перпендикулярами на координатные оси будут отрезки ААz ААу; АAх на координатные плоскости αху, Ауz АХz. Получаем что основания перпендикуляров: Аху(1;2;0), Аyz(0;2;3), Аxz(1;0;3).ответ:
Объяснение:
Объяснение:
1) 5х+3х+7х=45
х=3
Стороны: 15, 9, 21
2) 3х=5 5х=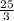 = 8
= 8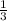
7х =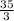 = 11
= 11
Стороны: 5, 8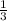 , 11
, 11
3) 7Х=7
Стороны: 5, 3, 7