Средняя линия треугольника соединяет середины двух сторон, параллельна третьей стороне и равна ее половине.
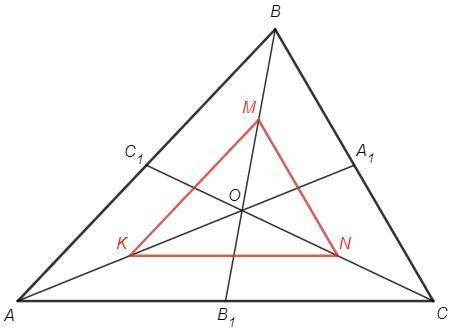
Отрезки KM, MN, KN являются средними линиями в треугольниках AOB, BOC, AOC.
a) KM||AB, MN||BC, KN||AC
KMN~ABC по трем параллельным сторонам
б) KM=AB/2, MN=BC/2, KN=AC/2
P(ABC) =2P(KMN) =44*2 =88 (см)
в) Отношение соответствующих отрезков (медиан, биссектрис, высот и любых отрезков, построенных сходным образом) в подобных треугольниках равно коэффициенту подобия.
k=AB/KM =2
Медианы ABC вдвое больше медиан KMN.
По теореме косинусов находим квадрат третей стороны треугольника:
ВС² = АВ²+АС²-2*АВ*АС*Cos45° = 128+324-2*8√2*18*0,707 =164.
Продолжаем медиану за точку пересечения с третей стороной и откладываем на продолжении отрезок, равный медиане. Имеем параллелограмм ( по признаку параллелограмма: если диагонали четырехугольника делятся в точке их пересечения пополам, то этот четырехугольник - параллелограмм). По свойству параллелограмма: "Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон" находим вторую диагональ (первая это ВС):
164+X² =2*(128+324), отсюда Х = √740 ≈ 27,2 Это две медианы, значит медиана равна 13,6.