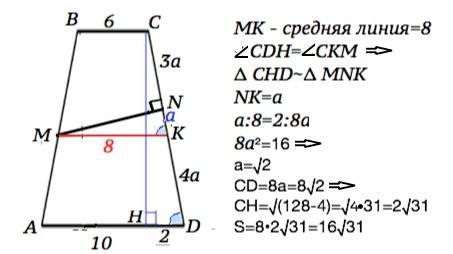
Проведем отрезок МК║АD. Так как М - середина АВ, МК- средняя линия трапеции. МК=(6+10):2=8
Примем коэффициент отношения СN:ND равным а.
Тогда СD=3a+5a=8a,
CK=KD=8a:2=4a, из чего следует NK=a.
Опустим высоту СН на АD.
Высота, проведенная из тупого угла равнобедренной трапеции, делит большее основание на отрезки, один из которых равен полуразности оснований, другой – их полусумме. =>
DH=(10-6):2=2, AH=MN=(10+6):2=8
МК║AD, СD – секущая => ∠CKM=∠CDA.
Прямоугольные ∆ СDH~∆ MKN по острому углу.
Из подобия следует: Отношение катетов к гипотенузе подобных прямоугольных треугольников равно.
NK:MK=HD:СD
a:8=2:8a
8a²=16 =>
a=√2 и СD=8√2
По т.Пифагора
CH=√(CD²-HD²)=√(128-4)=2√31
Площадь трапеции равна произведению высоты на полусумму оснований:
S=(2√31)•8=16√31 (ед. площади)
Принципат (лат. principatus, от princeps — первый сенатор, сенатор, открывающий заседание) — условный термин в исторической литературе для обозначения сложившейся в Древнем Риме в период ранней империи (27 год до н. э. — 284 год н. э.) особой формы монархии, совмещавшей монархические и республиканские черты. Обладатели высшей власти в основном именовались титулом принцепс, этим подчёркивался их статус не монарха-самодержца, а первого среди равных.
Объяснение:
Принципат (лат. principatus, от princeps — первый сенатор, сенатор, открывающий заседание) — условный термин в исторической литературе для обозначения сложившейся в Древнем Риме в период ранней империи (27 год до н. э. — 284 год н. э.) особой формы монархии, совмещавшей монархические и республиканские черты. Обладатели высшей власти в основном именовались титулом принцепс, этим подчёркивался их статус не монарха-самодержца, а первого среди равных.