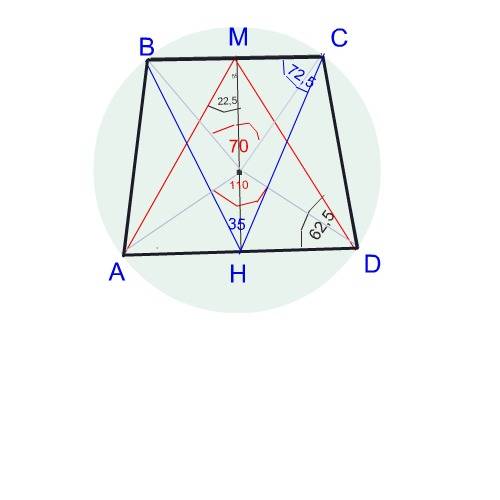
Рисуем трапецию в окружности.
Дополним рисунок треугольниками АМD и ВНС.
Углы при вершинах этих треугольников равны половине центральных углов ( под которыми видны из центра окружности основания трапеции)
Путем несложных вычислений находим углы треугольников DМН и МНС
Для решения применена теорема синусов.
Синусы найденных углов
72,5=0,9537
62,5=0,8870
22,5=0,3826
17,5=0.3007
---------------------------------
МН:sin 62,5=8:0,887=9,019
DН=9,019∙ sin22,5=3,4507
AD=6,9
-------
МН:sin 72,5=8:0,9537=8,3884
СМ=8,3884∙sin17,5=2,52
ВС=5,04
Ясно, что значения длин сторон округленные.
-------------
Площадь трапеции равна произведению полусуммы оснований на ее высоту.
S ABCD=8(6,9+5,04):2=95,52 (?)³
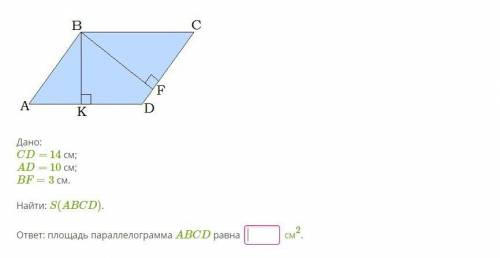
Пусть трапеции ABCD, где прямой угол - А.. Проведём высоту из т. С. Назовём её СО. Бис-са выходит из угла D. Тогда
1)угол DBC=BDA, Тк являбтся накрест лежащимт при прямых BC И AD И секущей BD. Тогда получается, что треуг BD равнобедренный.
2) в ранобедренном трег боковые стороны равны. BC=CD=15см.
3) рассмотрим прямоуг. ABCO. В прямоуг противолежсщие стороны равны. AB=CO=12, BC=AO=20.
4) рассмотрим треуг COD. По теореме Пифагора ОD^2= 225-144=81. Значит OD=9см.
5) AD=20+9=29см.
6) SABCD=(20+29)/2*12=39/2*12=39*6=234 СМ ^2
Вроде так, надеюсь правильно, ту тему чам не очень понял
Объяснение:
140 cm2