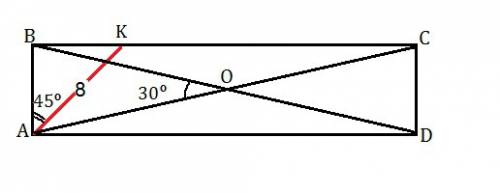
В прямоугольнике ABCD проведена биссектриса угла A до пересечения со стороной BC в точке K. Отрезок AK=8 см, угол между диагоналями прямоугольника равен 30°. Найдите стороны и площадь прямоугольника ABCD.
Обозначим точку пересечения диагоналей О.
Диагонали прямоугольника равны и точкой пересечения делятся пополам.
∆АОВ и ∆COD - равнобедренные, углы при АВ и CD равны по (180°-30°):2=75°⇒
в ∆ АВС ∠BСA=90°-75°=15°
∆ АВК - прямоугольный с острым углом ВАК=45°⇒
∠ВКА=45° ⇒ ∆ АВК равнобедренный.
АВ=АК*sin45°=(8*√2)/2=4√2 см
В ∆ АВС по т.синусов
АВ:sin15°=BC:sin75°
По таблице синусов
sin 15° =0,2588
sin75°=0,9659
4√2:0,2588=ВС:0,9659⇒
ВС=21,1127 см
S=AB•ВС=4√2•21,1127≈ 119,426 см²
------
Как вариант:
Найти из прямоугольного ∆ АВС диагональ АС:
АС=АВ:sin 15º=(4√2):0,2588
Площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними.
S=0,5•d₁•d₂•sinφ , где
d₁ и d₂ – диагонали, φ – любой из четырёх углов между ними/
Тогда S=0,5•{4√2):0,2588}²•0,5=≈ 119,426 см²
Объяснение:
1)
Дано:
Параллелограм
S=48см
h(a)=2см
h(b)=6см
а=?
b=?
_________
Площадь параллелограма равна произведению высоты на сторону, на которую опущена эта высота
S=а*h(а)
Отсюда
а=S/h(a)=48/2=24 см сторона параллелограма
b=S/h(b)=48/6=8 см сторона параллелограма.
ответ: 24см; 8см.
2)
Дано:
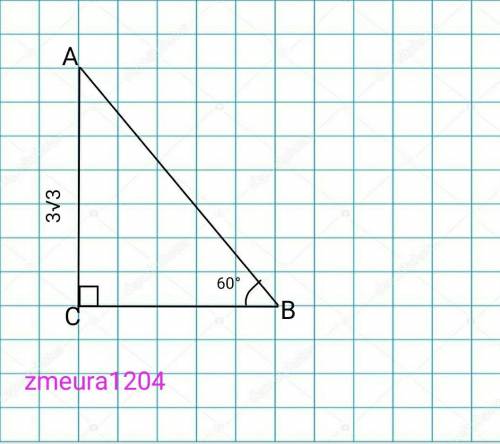
АВС- прямоугольный треугольник
АС=3√3см
<АВС=60°
АВ=?
СВ=?
_________
sin<B=AC/AB
√3/2=3√3/AB
AB=3√3*2/√3=6см.
tg60°=AC/CB
√3=3√3/CB
CB=3√3/√3=3см.
S=1/2*AC*CB=1/2*3√3*3=4,5√3 см²
ответ: СВ=3см; АВ=6см; S=4,5√3см²
3)
Дано:
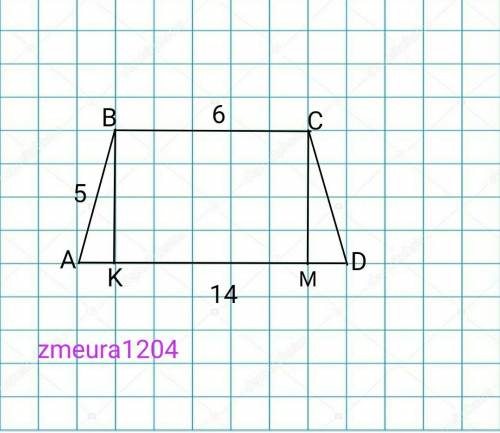
ABCD- трапеция.
ВС=6см
АD=14см
АВ=СD=5см
S=?
_______
Решение
АК=МD
AK=(AD-BC)/2=(14-6)/2=8/2=4 см.
∆АКВ- прямоугольный треугольник.
По теореме Пифагора
ВК=√(АВ²-АК²)=√(5²-4²)=√(25-16)=√9=3 см
S=BK(BC+AD)/2=3(6+14)/2=3*20/2=30см²
ответ: 30см²
Решено zmeura1204.
б.Корені 13 це правильна відповідь