ответ: S= 420
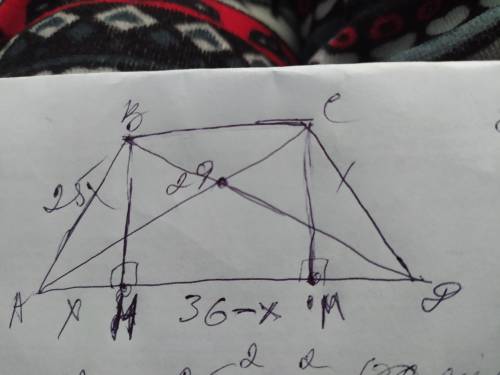
Объяснение: Проведём от вершины В высоту ВН. К нам получилось 2 прямоугольных треугольника АВН и ВДН. Пусть отрезок АН=х, тогда отрезок ДН=36-х. Высота ВН является общей стороной этих треугольников. Составим уравнение по теореме Пифагора:
25^-х^=29^-(36-х)^
625-х^=841-(1296-72х+х^)
625-х^=841-1296+72х-х^
-х^+х^-72х=841-1296-625
-72х= - 1080
х= - 1080÷(-72)
х=20
Мы нашли высоту ВН =20.
Теперь найдём ВС - верхнее основание.
Проведём ещё одну высоту СМ от вершины С к нижнему основанию трапеции. Две высоты отсекают он нижнего основания отрезок равный верхнему основанию:
ВС=НМ=36-2×15=36-30=6; ВС=НМ=6
Теперь найдём площадь трапеции:
S=1/2(АД+ВС)×ВН:
(36+6)÷2×20=42÷2×20=21×20=420
1)Треугольник AOB равен тр-ку COD по 2 сторонам и углу между ними. Т.к они равны, то соотв. элем. равны. Угол OCD равен углу OBA - они накрест лежащие при прямых АВ и CD и сек. ВС. Следовательно, AB ║CD
2)Треугольники OXY и OZY равны по 3 сторонам. Т.к они равны, то соотв. элем. равны. Угол XOY равен углу YZO - они накрест лежащие при прямых OX и YZ и сек. OY. Следовательно, OX ║YZ. Также угол XYO = углу YOZ(из равенства тр-к) - они накрест лежащие при прямых OX и YZ и сек. OY. Следовательно, OZ ║XY
3)Треугольники ROB и SOT равны по стороне и двум прилежащим к ней углам. Т.к они равны, то соотв. элем. равны. Угол BRO = углу STO - они накрест лежащие при прямых RB и ST и сек. BS. Следовательно, RB ║ST. Также треугольники ROS и BOT равны по стороне и 2 прилежащим к ней углам. Отсюда угол SRO = углу BTO - они накрест лежащие при прямых RS и BT и сек. RT. Следовательно, RS ║BT.