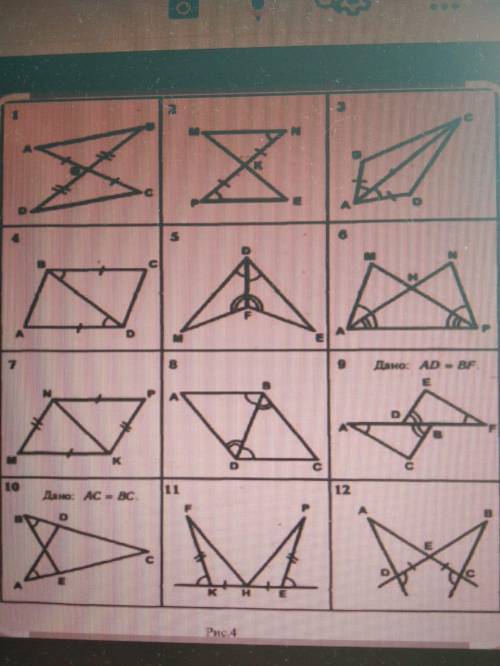
Теорема. Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.
Доказательство.
Проведем высоты ВН и СЕ. Докажем, что S(ABCD) = AD · BH.
ΔАВН = Δ DCE - они прямоугольные и равны по гипотенузе (АВ = СD как противоположные стороны параллелограмма) и катету (ВН = СЕ как перпендикуляры, проведенные от одной из параллельных прямых к другой). Значит, равны и их площади (есть аксиома площади: равные фигуры имеют равные площади), т.е. S(ABH) = S(DCE).
Заметим, что S(ABCD) =S(ABCЕ) - S(DСЕ),
а также S(НBCЕ) = S(ABCЕ) - S(ABН).
Откуда следует, что S(ABCD) = S(НBCЕ) , т.к. выше доказано, что S(ABH) = S(DCE). Но НВСЕ - прямоугольник, а площадь прямоугольника равна произведению двух его сторон (доказывается ранее при изучениии темы "Площпди многоугольников"), т.е. S(НBCЕ) =AD · BH.
Следовательно, и S(ABCD) = AD · BH.
Теорема доказана.
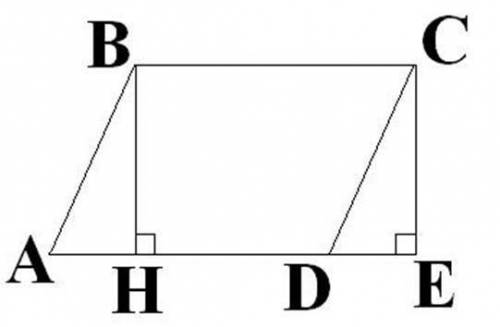
1)по первому признаку
2)по второму
3)по первому
4)по первому
5)по второму
6)по второму
7)по третьему
8)по второму
9)по второму
10)по второму
11)по первому
12)по второму
Объяснение:
1)АО=ОС, ВО=ОД, <АОД=<ВОС(Как вертикальные)
2)NК=КР, <N=<Р, <NКМ=<ЕКР(как вертикальные)
3)АВ=АД, <САВ=<САД, АС-общая
4)ВС=АД, ВД-общая, <СВД=<АДВ
5)<MDF=<EDF, <EFD=<MFD, DF-общая
6)<AFM=<FAM, <AFN=<FAH, AF-общая
7)МК=РN, NМ=РК, NK-общая
8)<АВД=<СДВ, <СВД=<АДВ, ВД-общая
9)<EFD=<CAB, <CBA=<FDE, AB=AD+DB=FB+BD, значит АВ=FD
10)<DAC=<CBE, AC=BC, <C-общий
11)PE=FK, EH=HK, <PEH=<FKH(как смежные равным углам)
12)EC=ED, <AED=<BEC(как вертикальные), <BCE=<ADE(как смежные при равных углах)