По условию, МСН = 13°.
1) Сумма острых углов СМН, МСН прямоугольного треугольника НСМ равна 90o. Значит, СМН = 90o - МСН = 90o - 13o = 77o
2) Треугольник АМС равнобедренный, т.к. СМ равна половине гипотенузы по свойству из п.3 "Что необходимо знать для решения", а АМ равна половине гипотенузы, т.к. СМ - медиана. Отсюда следствие: угол А равен углу АСМ по свойству углов при основании равнобедренного треугольника.
3) Угол СМН внешний по отношению к треугольнику АМС. Он равен сумме двух внутренних А и АСМ, с ним не смежных. Но А = АСМ как углы при основании равнобедренного треугольника. Следовательно, А = АСМ = 77o : 2 = 38,5o
4) Один острый угол А треугольника АВС мы нашли. Теперь найдем второй. Сумма острых углов А, В прямоугольного треугольника АВС равна 90o. Значит, В = 90o - А = 90o - 38,5o = 51,5o
Больший угол равен 51,5o.
ответ: 51,5°
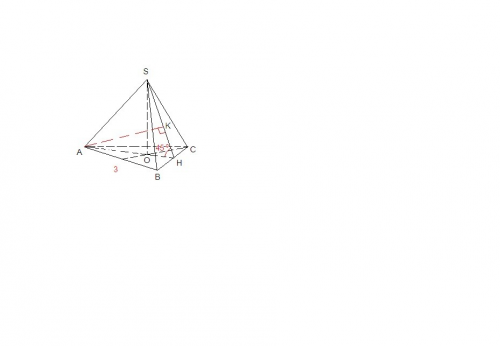
Центр шара лежит в точке, равноудалённой от сторон треугольника, образуя вместе с вершинами треугольника треугольную пирамиду с равными апофемами. Апофемы равны, значит основание высоты пирамиды лежит в центре вписанной в основание пирамиды окружности.
Площадь основания можно вычислить по формуле Герона:
S=√(p(p-a)(p-b)(p-c)), где р=(a+b+c)/2.
Подставив числовые значения a=13, b=14 и с=15 получим S=84 см.
Радиус вписанной окружности: r=S/p=2S/(a+b+c).
r=2·84/(13+14+15)=4 см.
Высота пирамиды, проведённая к данному треугольнику - это расстояние от центра шара до треугольника.
В прямоугольном треугольнике, образованном высотой пирамиды, апофемой и найденным радиусом, высота по теореме Пифагора равна:
h=√(l²-R²), где l- апофема пирамиды (равна радиусу шара).
h=√(4²-3²)=7 см - это ответ.