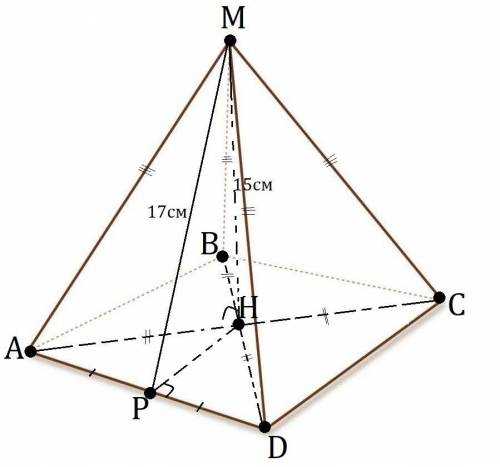
В правильной пирамиде высота падает в центр основания, то есть в центр правильного многоугольника. Правильный четырёхугольник это квадрат, а его центр находится на пересечении диагоналей. Боковые грани правильной пирамиды это равнобедренные треугольники, которые равны. Апофема это высота боковой грани. В квадрате все стороны равны, диагонали равны и делятся точкой пересечения пополам.
Пусть P∈AD и MP⊥AD, тогда MP=17см и AP=PD т.к. в равнобедренном Δ высота является и медианой.
Пусть H∈(ABC) и MH⊥(ABC), тогда AC∩BD=H.
ΔMHP - прямоугольный, найдём неизвестный катет.
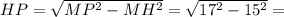
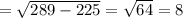 см.
см.
ΔAHD - равнобедренный, поэтому PH не только медиана, но и высота.
ΔHPD - прямоугольный, ∠HDP=45° т.к. диагонали квадрата являются и биссектрисами, значит HP=PD=8см - равны как катеты, прямоугольного Δ с острым углом в 45°.
AD=2·PD=2·8см=16см.
Площадь квадрата можно найти через сторону, а площадь равнобедренного треугольника через сторону и высоту опущенную на эту сторону.
S(ABCD) = AD²=16² см².
S(AMD) = MP·AD:2=17·16:2 см².
S(бок. пов.) = 4·S(AMD)=4·17·16:2 см²=2·17·16 см².
S(полн. пов.) = S(ABCD)+S(бок. пов.) = 16²см²+2·17·16 см² = 32·(8+17)см² = 8·4·25см²=800см².
ответ: 800см².
a) b;
B)
г) п.
a
+
m
А6. Отрезок МN является средней линией треугольника ABC. Число k, для которого vec AB =k* vec MA , равно:
а) 2,
6) -2;
1 2 ;
r)- 1 2 .
A7. ABCD параллелограмм, O - roq пересечения его диагоналей. Тогда верным будет равенство:
a) vec AO - vec OD = vec AD
6)
vec AO - vec BO = vec AD
;
B) vec AB + vec BO = vec AO ;
г) vec AB + vec BO = vec AC .
. А8. В четырехугольнике АBCD vec AB = vec DC точка K-* cepe дина AD. Прямая СК пересекает прямую ВА в точке N. Среди указанных пар векторов не являются коллинеар ными векторы:
a) vec AD u vec NK
б) vec AK u vec BC ;
в) vec AK u vec DA ;
г) vec BN H vec DC
B
M
C
A
N
Решите это пжА5. На рисунке изображены векторы. Вектор, равный век тору 3 overline a , будет векто
Решите это пжА5. На рисунке изображены векторы. Вектор, равный век тору 3 overline a , будет векто
Все ответы