
∠A=∠D=74°
∠B=∠C=106°
Объяснение:
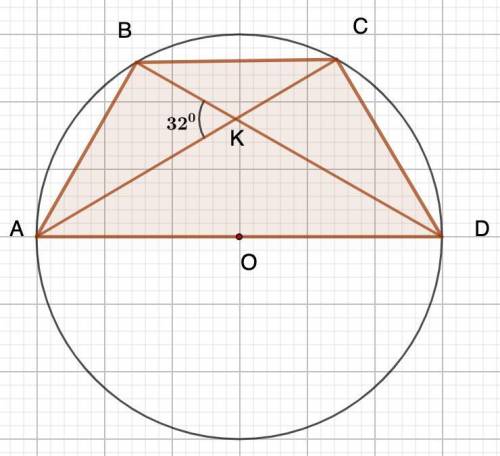
Дано: Окр.О
ABCD - вписанная трапеция.
∠АКВ=32°
О∈AD
Найти: углы трапеции.
1) ABCD - равнобедренная трапеция (вписанная)
∠АКВ=(∪AB+∪CD):2 (угол между пересекающимися хордами)
∪AB=∪CD (равными хордами стягиваются равные дуги)
32°=(∪AB+∪CD):2
2∪АВ=64° ⇒ ∪АВ=∪CD=32°
2) ∠ABD=90° (вписанный, опирается на диаметр)
∠DBC=∪CD:2=32°:2=16° (вписанный)
⇒∠B=∠ABD+∠DBC=90°+16°=106°
3) ∠A=180°-∠B=180°-106°=74° (внутренние односторонние при BC║AD и секущей АВ)
4) Углы при основаниях равнобедренной трапеции равны.
∠A=∠D=74°
∠B=∠C=106°
угол A равен 470 . Найдите угол C и угол B.
2. AB и AC – отрезки касательных, проведенных к окружности радиуса 6 см. Найдите длинуOA и AC, если AB = 8 см.
3. Точки A и B делят окружность с центром O на дуги AMB и ACB так, что дуга ACB на 800меньше дуги AMB. AM – диаметр окружности. Найдите углы AMB, ABM, ACB.
4. Найдите радиус окружности, вписанной в треугольник, и радиус окружности, описанной около треугольника, стороны которого равны 16 см, 17 см и 17 см.
Контрольная работа № 5 по теме: «Окружность» Вариант 2
1. Дана окружность с центром в точке O. AB –диаметр, точка C отмечена на окружности,