1) кг
2) литры
3) Свойства объемов тел
Объем тела есть неотрицательное число;
Если геометрическое тело составлено из геометрических тел, не имеющих общих внутренних точек, то объем данного тела равен сумме объемов тел его составляющих;
Объем куба, ребро которого равно единице измерения длины, равен единице;
Равные геометрические тела имеют равные объемы.
4)Две фигуры называются на плоскости (в пространстве) называются равновеликими, если их площади (объемы) равны. * Любые две простые равновеликие фигуры на плоскости (в том числе, например, равновеликие многоугольники) равносоставлены.
5)Две фигуры и называются подобными, если существует подобие, переводящее одну из них в другую. Подобием называется преобразование пространства, при котором расстояния между точками изменяются в одно и то же число раз
6) Две фигуры называются подобными, если они переводятся одна в другую преобразованием подобия. ... Подобием называется преобразование пространства, при котором расстояния между точками умножаются на одно и то же положительное число
7) Для подобных фигур на плоскости, имеющих площадь, верна теорема: отношение площадей подобных фигур равно квадрату коэффициента подобия. Для подобных пространственных тел, имеющих объем, верна аналогичная теорема: отношение объемов подобных тел равно кубу коэффициента подобия.
8) цилиндр, конус
Объяснение:
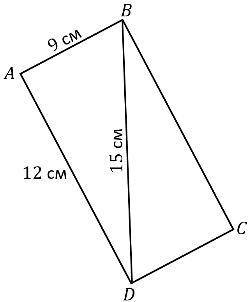
7. В треугольниках △ABD и △CBD DC=AD, AB=BC по условию, BD - общая сторона, значит △ABD=△CBD по 3му признаку. => <ABD=<CBD
8. В треугольниках △ABC и △ADC <BAC=<CAD, <BCA=<DCA по условию, АС - общая сторона, значит △ABC=△ADC по 2му признаку. => AD=AB=9cм, CD=BC=3см, АС (общая) =10см.
Р(ADC)=AD+CD+AC=9+3+10=22см
9. <OCN=<ONC => △CON - равнобедренный и тогда OC=ON.
Тогда в треугольниках △DCO и △DNO СD=DN по условию, OC=ON по доказанному выше, OD - общая сторона => △DCO=△DNO по 3му признаку.
9 см
Объяснение:
Расстоянием от точки до прямой является перпендикуляр, опущенный из данной точки на заданную прямую
В данном случае СD⊥AD. CD - искомое расстояние
Т.к. ABCD прямоугольник, то AB=CD = 9 см