Дано: АВС-прямоугольный треугольник
ВК=КС, т.к. АК-медиана
угол А=90 град.
ВС=60см
1.Если это прямоугольный треугольник, то допустим угол при вершине В=30град, а в следствии при вершине С=60град, при этом раскладе углов катет АС, лежащий напротив угла в 30град= половине гипотенузы, т.е =30см.
2. Медиана по своим свойства делитгипотенузу пополам, т.е. ВК=КС=30см.
3. Рассмотрим образовавшийся треугольник АКС, у него: КС=30см, АС=30см, значит треугольник АКС- равнобедренный, а угол С=60град, далее...
т.к. АКС - равнобедренный треугольник угол КАС=углу АКС=(180-уголС):2=(180-60):2=60град. Значит треуг АКС равносторонний, т.к все углы у него равны, отсюда АК=КС=АС=30см
ответ:АК=30см.
Объяснение:
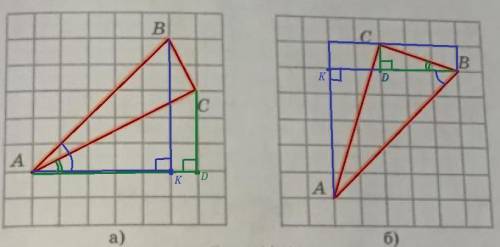
Тангенс угла в прямоугольном треугольнике - это отношение противолежащего катета к прилежащему. Проведём дополнительные прямые линии так, чтобы получить прямоугольные треугольники, из которых можно будет найти катеты необходимых углов и воспользуемся формулами тангенса суммы и разности углов.
а)
tg∠A = BC / AC = 3/6 = 1/2
ctg∠A = AC / BC = 6/3 = 2
б)
tg∠B = AC / BC = 4/6 = 2/3
ctg∠B = BC / AC = 6/4 = 3/2
№2
Тангенс угла в прямоугольном треугольнике -это отношение противолежащего катета к прилежащему. Проведём дополнительные прямые линии так, чтобы получить прямоугольные треугольники, из которых можно будет найти катеты необходимых углов и воспользуемся формулами тангенса суммы и разности углов.
tg(a-β)=tga-tgβ/1+tga×tgβ; tg(a+β)= tga+tgβ/1-tga×tgβ
a)tg ∠BAC = tg(∠BAD-∠CAD) =tg∠BAD- tg-∠CAD/1+tg∠BAD×tg∠CAD=∠BAD= BK/AK=5/5=1; tg∠CAD= CD/AD=3/6=1/2=1-1/2/1+1×1/2=1/2/3/2=1/3
ctg∠BAD=1/tg∠BAD=1/1/3
b) tg∠ABC=tg(∠CBD+∠KBA) =tg∠CBD+tg∠KBA/1-tg∠CBD×tg∠KBA=tg∠CBD=CD/BD=1/3; tg∠KBA=AK/BK=5/5=1=1/3+1/1-1×1/3=4/3/2/3=4/2=2