Апофема наклонной боковой грани данной пирамиды - есть гипотенуза прямоугольного треугольника, построеного на высоте ромба и высоте пирамиды как на катетах, угол между апофемой и плоскостью основания равен 30⁰, против этого угла лежит катет 4 см, значит апофема равна 8 см
Из этого же треугольника, высота ромба равна:
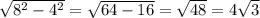 см
см
Острый угол ромба равен 60⁰, ребро ромба (обозначим за Х) равно:
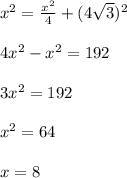
Ребро ромба равно 8 см.
Площадь боковой поверности пирамиды:
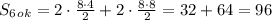 см²
см²
Очень подробно нет времени расписывать, слишком много заданий ещё делаю, но ход решения именно такой. Лучше нарисовать рисунок, будет понятнее.
Для того, чтобы правильно решить это задание нужно точно представлять, что именно является расстоянием между прямыми DB и AC, недаром наи даны в условии все длины рёбер пирамиды.
В треугольниках АВС и ADC провёдём высоты ВО и DО, которые обе являются перпендикулярами к АС.
Таким образом, прямая АС перпендикулярна плоскости DВО (на рисунке - жёлтым), согласно признака перпендикулярности прямой и плоскости.
Высота ОН (на рисунке - красным) треугольника DВО перпендикулярна к АС и к DВ, а значит и является искомым расстоянием.
Ну и далее, собственно, сами рассчёты:
ΔАВС=ΔАDС по трём сторонам, значит высоты ВО и DO равны, оба треугольника - равнобедренные, значит высоты являются медианами, и равны:
ΔDBO также равнобедренный, и точно также находим ОН:
Как "Лучшее решение" не забудь отметить, ОК?!.. ;)))