угол А - 36 градусов, угол В - 27 градусов, угол С - 117 градусов.
Объяснение:
1. По теореме косинусов: а^2 + b^2 + c^2 = 2 x b x c x cos C
cos C = (b^2 + c^2 - a^2) / 2 x b x c
cosC = (4^2 + 6^2 - 3^2) / 2 x 4 x 6
(16 + 36 - 9) / 48 = 43 / 48 = 0.8958
угол С по таблице Брадиса примерно равен 27 градусов.
2. соs A = cos C = (a^2 + c^2 - b^2) / 2 x a x c
cosA = (3^2 + 6^2 - 4^2) / 2 x 3 x 6 = (9 + 36 - 16) / 36 = 29 / 36 = 0.8055
угол A по таблице Брадиса примерно равен 36 градусов.
3. Угол В = 180 - А - С = 180 - 36 - 27 = 117
Объяснение:
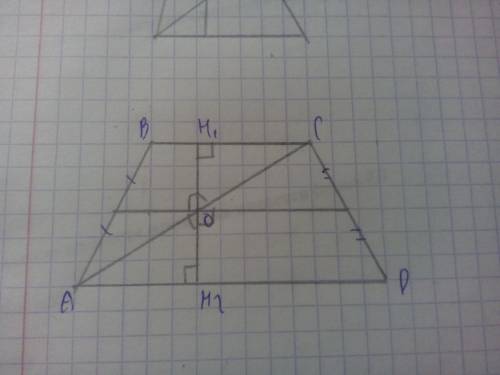
Проведём перпендикуляр в точке О. Я его назвал H1H2. Точка О лежит на средней линии трапеции (так как концы этого отрезка на серединах сторон). Средняя линия параллельна основаниям (такое свойство у средней линии трапеции). Значит H1H2 перпендикулярно и средней линии и основаниям.
Докажем, что H1O=H2O, это можно сделать по теореме Фалеса, утверждающей, что параллельные прямые отсекают на секущих равные отрезки, (отрезки на боковой стороне равны, значит и на перпендикуляре равны).
И теперь рассматриваем треугольники AOH2 и COH2, о чудо они равны по 2 углам и стороне между ними (OH2=OH1, только что доказали, угол AH2O=OH1C=90 (там перпендикуляры), угол AOH2=COH1 как вертикальные)
А если треугольники равны, то и стороны против равных углов в них равны (есть такая теорема) значит и AO=OC равны ч.т.д.
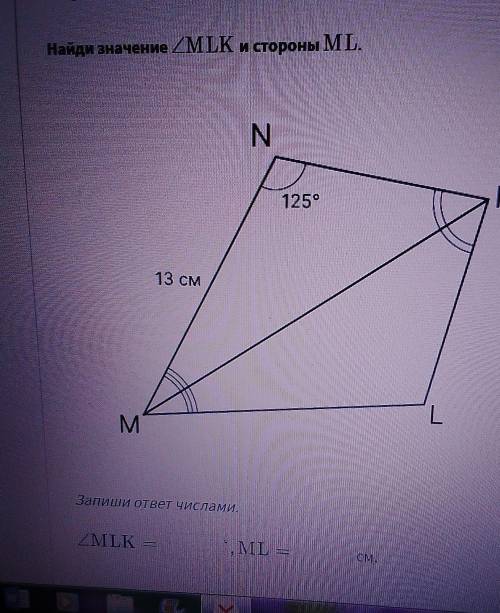
∠MLK = 125°; ML = 13 см
Объяснение:
Дано: MNKL.
∠N = 125°; MN = 13 см;
∠1 = ∠2; ∠3 = ∠4.
Найти: ∠MLK; ML.
Рассмотрим ΔMNK и ΔMKL.
∠1 = ∠2; ∠3 = ∠4 (условие)
МК - общая
⇒ ΔMNK = ΔMKL (по стороне и двум прилежащим углам, 2 признак)
В равных треугольниках против равных сторон лежат равные углы, а против равных углов лежат равные стороны.⇒ ∠MLK = ∠MNK = 125°; ML = MN = 13 см