-Длина отрезка ОВ равна длине отрезка ОС как радиусы окружности.
ОВ = ОС = 4 см.
-Радиусы ОВ и ОС проведены к точкам касания В и С касательных АВ и АС, тогда радиусы ОВ и ОС перпендикулярны касательным АВ и АС, а тогда треугольники АОС и АОВ прямоугольные.
-Касательные АС и АВ проведены из одной точки А, тогда, по свойству касательных, АВ = АС.
-В прямоугольных треугольниках АОВ и АОС гипотенуза АО общая, катет ОВ = ОС, тогда треугольники АОВ и АОС равны по катету и гипотенузе.
Тогда угол ОАВ = ОАС = ВАС / 2 = 56 / 2 = 280.
ответ:280
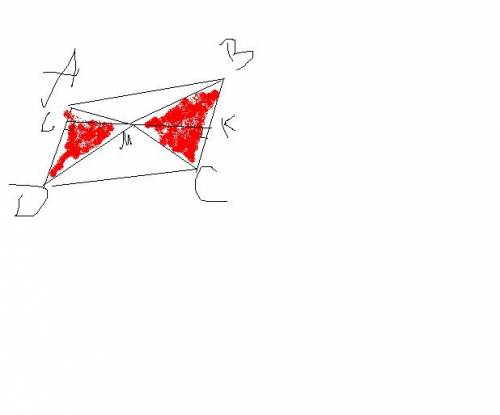
проведем через точку М, пряммую перпендикулярную АD, так как AD||BC, то она будет перпендикулярна и прямой ВС, пусть пряммую AD она пересекает в точке L, а пряммую BC в точке K.
Тогда LM - высота параллелограмма ABCD, LM - высота треугольника ADM, KM - высота треугольника BCM.
Площадь парарлелограмма равна произведению его стороны на высоту, проведенную к этой стороне
Площадь треугольника равна половине произведения стороны на высоту провдеенной к этой стороне
Поэтому
S(AMD)+S(BMC)=1/2*AD*LM+1/2*BC*KM=так противоположные стороны парарлелограмма равны=
=1/2*AD*LM+1/2*AD*KM=1/2*AD*(LM+KM)=1/2*AD*LK=1/2*S(ABCD), что и требовалось доказать
24
Объяснение:
1. А, В, С, Д - вершины трапеции. ВС = 2 единицы измерения. АД = 10 единиц измерения.
ВЕ - высота. S - площадь. ∠А = 45°.
2. Вычисляем длину отрезка АЕ основания АД:
АЕ = (АД - ВС)/2 (согласно свойствам равнобедренной трапеции).
АЕ = (10 - 2)/2 = 4 единицы измерения.
3. ВЕ/АЕ = тангенс ∠А = тангенс 45° = 1.
ВЕ = АЕ х 1 = 4 х 1 = 4 единицы измерения.
4. S = (АД + ВС)/2 х ВЕ = (10 + 2)/2 х 4 = 24 единицы измерения².
ответ: S равна 24 единицы измерения².