Question

РЕШИТЕ Вариант 2 1.Найдите второй катет прямоугольного треугольника, если его гипотенуза 17 см, а
друтой катет 15 см.
2. Диагонали ромба равны 14см. и 48 см. Найдите сторону ромба.
3. В параллелограмме две стороны 12см. и 16 см., а один из углов 150°. Найдите площадь
параллелограмма.
4.В треугольнике ABC ZA = 30°, ZB = 75°, высота BD равна 6 см. Найдите площадь
треугольника ABC.
5.Диагональ прямоугольника равна 13 см, а одна из сторон – 5 см. Найдите площадь и
периметр прямоугольника.
6. В равнобедренной трапеции боковая сторона равна 13 см, основания 10 и 20 см.
Найдите площадь трапеции.

Answer 1

1. $\sqrt{17^2-15^2}$=8 см

2. $\sqrt{(14/2)^2+(48/2)^2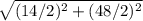}$=25 см

3. S=a*h=12*8=96 см²

h=16*sin30°=8 см

4. S=в*h/2=12*6/2

а=h/sin30°

а=в

∠В=∠С

5. в=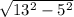$\sqrt{13^2-5^2}$=12 см

S=a*в=12*5=60 см²

p=2(5+12)=34 см

6. h=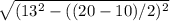$\sqrt{(13^2-((20-10)/2)^2}$=12 см

S=(20+10)/2*12=180 см²

Объяснение: