22√7
Объяснение:
Формула для нахождения площади трапеции через ее основания и высоту:
S =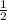 
* (a + b) * h, где a, b — основания трапеции, h — высота трапеции.
СН ⊥ АД, СН - высота трапеции.
Рассмотрим ΔСДН(∠Н=90°).
СН = sin ∠Д * СД,
НД = cos ∠Д * СД.
Воспользуемся формулами приведения:
соsC = соs( 180°-∠Д) = - соs ∠Д ⇒ соs ∠Д = - соsC = 3/4
sin² ∠Д = 1 - соs² ∠Д = 1 - 9/16 = 7/16
sin ∠Д = 
= √7 / 4
СН = (√7 / 4 )* 8 = 2√7
НД = 3/4 * 8 = 6
т.к. трапеция АВСД - равнобокая, то АД = ВС+2*НД = 5+2*6=17 см
S = 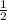* (5+17)* 2√7 = 22√7
Есть 2 вариант.
После того, как нашли НД, через cos ∠Д, воспользоваться т. Пифагора и найти СН из ΔСДН :
СН² = СД²-НД² = 64-36 = 28
СН = √28= 2√7
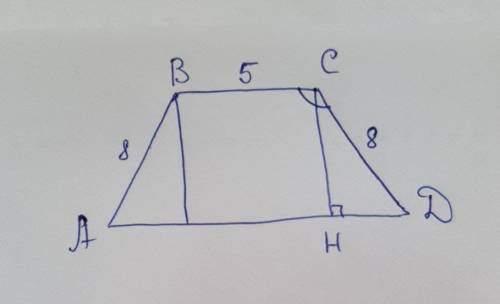
ABCD- равнобедрренная трапеция, BC и AD - основания трапеции, BD=10м - диагональ, ВК - высота, угол BDK=60 градусов. Рассм треугольник BKD - прямоугольн.т.к. BK перпендикулярно AD. sinBDK=BK/BD, BK=sin60*BD=(корень из 3)/2*10=5 корней из 3. По т. Пифагора BD^2=BK^+KD^2, KD^2=BD^-BK^, KD^=100-75=25. KD=5. По свойствам равнобедренной трапеции (Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой - полуразности оснований.) KD=(BC+AD)/2=5. Тогда S=(BC+AD)/2*BK=5*5корней из 3=25 корней из3.