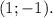Объяснение:
1) Найдем разность арифметической прогрессии
d = a3 - a2 = 6,8 - 4,5 = 2,3
а1= а2 - d = 4,5 - 2,3 = 2,2
а4 = а1 + 3d = 2,2 + 2,3 * 3 = 9,1
a5 = a1 + 4d = 2,2 + 2,3 * 4 = 11,4
2) а2 = -7; а3 = - 25
d = a3 - a2 = -25 - (-7) = -18
а1= а2 - d = -7 - (-18) = 11
а4 = а1 + 3d = 11 + (-18) * 3 = -43
a5 = a1 + 4d = 11 + (-18) * 4 = -61
3) а2 = 24,6 ; а3 = 19
d = a3 - a2 = 19 - 24,6 = - 5,6
а1= а2 - d = 24,6 - (-5,6) = 30,2
а4 = а1 + 3d = 30,2 + 3 * (-5,6) = 13,4
a5 = a1 + 4d = 30,2 + 4 * (-5,6) = 7,8
4) а2= 0,48; а3 = 0,31
d = a3 - a2 = 0,31 - 0,48 = - 0,17
а1= а2 - d = 0,48 - (-0,17) = 0,65
а4 = а1 + 3d = 0,65 + (- 0,17) * 3 = 0,14
a5 = a1 + 4d = 0,65 + (- 0,17) * 4 = -0,03
5) а2= -57,5 а3= - 68
d = a3 - a2 = - 68 - (-57,5) = - 10,5
а1= а2 - d = -57,5 - (-10,5) = - 47
а4 = а1 + 3d = -47 + (-10,5) * 3 = - 78,5
a5 = a1 + 4d = -47 + (-10,5) * 4 = - 89
Объяснение:
Расстояние между двумя точками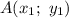
и 
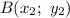находится по формуле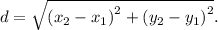 
Поэтому
Уравнение прямой, проходящей через точк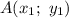и
и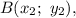 
имеет вид
поэтому уравнение прямой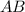
Угловой коэффициент найденной прямой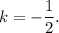
Так как стороны квадрата перпендикулярны, уравнения прямых, которые их выражают, должны удовлетворять условию перпендикулярности с заданной прямой (для перпендикулярных прямых с угловыми коэффициентам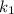и
и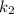 
выполняется равенство 
).
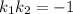Тогда угловой коэффициент прямых, проходящих перпендикулярно отрезку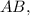
равен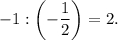 
Значит все такие прямые имеют вид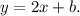
Подставив координаты точки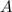
в полученное уравнение, найдем
Значит уравнение прямой, перпендикулярной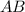
и проходящей через точку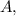 
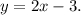
Аналогично подставив координаты точки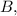
получим
Значит уравнение прямой, перпендикулярной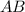
и проходящей через точку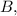 
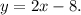
Таким образом, точка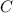
лежит на прямой 
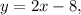т. е. ее координаты 
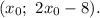А длина стороны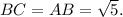 
Пользуясь формулой расстояния между двумя точками (см. выше), получаем:
Вычисляем соответствующие значения y для этих точек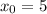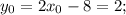: для
для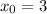 
Выходит, два возможных положения точки C —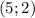
или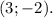 
Проделываем ту же последовательность действий для определения координат точки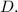
Так как она лежит на прямой 
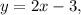то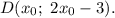 
тогда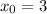 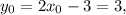для
а для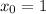 
Значит возможные положения точки 
— 
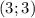или 