ответ:Дан ромб, сторона которого равна 17 см, а разность диагоналей - 14 см.
Диагонали d1 и d2 ромба перпендикулярны, образуют 4 треугольника.
По заданию d1 - d2 = 14. Разделим на 2 обе части.
(d1/2) - (d2/2) = 7.
Обозначим (d1/2) за х - это катет треугольника.
Второй катет равен х - 7.
По Пифагору a ² = (d1/2) ² + (d2/2) ².
289 = x² + (x - 7) ².
289 = x² + x² - 14x + 49.
2x² - 14x = 240 разделим на 2 и получаем квадратное уравнение.
х² - 7 х - 120 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D = (-7) ^2-4*1 * (-120) = 49-4 * (-120) = 49 - (-4*120) = 49 - (-480) = 49+480=529;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1 = (√529 - (-7)) / (2*1) = (23 - (-7)) / 2 = (23+7) / 2=30/2=15;
x_2 = (-√529 - (-7)) / (2*1) = (-23 - (-7)) / 2 = (-23+7) / 2=-16/2=-8.
Один катет получен: (d1/2) = 15 см, второй равен 15 - 7 = 8 см.
Площадь ромба равна:
S = 4 * (1/2) * 15*8 = 15*16 = 240 см².
Объяснение:
∠А = 36,34°; ∠В = 117,28°; ∠С = 26,38°.
Объяснение:
1) По теореме косинусов:
a^2 = b^2 + c^2 + 2bc*cos (α),
откуда
cos (α) = (b^2 + c^2 - a^2) / 2bc .
2) Обозначим углы и стороны:
∠ А = α
∠ В = β
∠ С = Δ
а = ВС (лежит против угла α)
b = АС (лежит против угла β)
с = АВ (лежит против угла Δ).
3) cos (α) = (b^2 + c^2 - a^2) / 2bc = (6^2 + 3^2 - 4^2) / (2*6*3) =
(36+9-16)/36 = 29/36 = 0,8055 55
По таблице косинусов находим, какой это угол:
α = arccos 0,8055 55 = 36,34°.
∠А = 36,34°.
4) Находим второй острый угол (он лежит против стороны 3 см и должен получиться меньше угла α):
cos (Δ) = (b^2 + а^2 - с^2) / 2ab = (6^2 + 4^2 - 3^2) / (2*6*4) =
(36+16-9)/48 = 43/48 = 0,8958 33
По таблице косинусов находим, какой это угол:
α = arccos 0,8958 33 = 26,38°.
∠С = 26,38°.
5) Находим третий угол:
180 - 36,34 - 26,38 = 117,28°.
∠В = 117,28°.
ответ: ∠А = 36,34°; ∠В = 117,28°; ∠С = 26,38°.
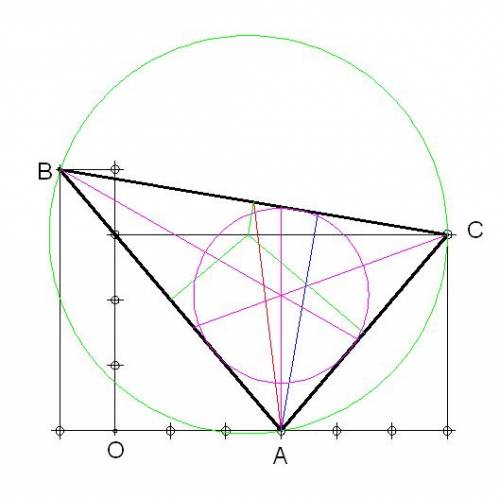
РАСЧЕТ ТРЕУГОЛЬНИКА
заданного координатами вершин:
Вершина 1: A(3; 0)
Вершина 2: B(-1; 4)
Вершина 3: C(6; 3)
ДЛИНЫ СТОРОН ТРЕУГОЛЬНИКА
Длина BС (a) = 7,07106781186548
Длина AС (b) = 4,24264068711928
Длина AB (c) = 5,65685424949238
ПЕРИМЕТР ТРЕУГОЛЬНИКА
Периметр = 16,9705627484771
ПЛОЩАДЬ ТРЕУГОЛЬНИКА
Площадь = 12
УГЛЫ ТРЕУГОЛЬНИКА
Угол BAC при 1 вершине A:
в радианах = 1,5707963267949
в градусах = 90
Угол ABC при 2 вершине B:
в радианах = 0,643501108793284
в градусах = 36,869897645844
Угол BCA при 3 вершине C:
в радианах = 0,927295218001612
в градусах = 53,130102354156
ЦЕНТР ТЯЖЕСТИ
Координаты Om(2,66666666666667; 2,33333333333333)
ВПИСАННАЯ ОКРУЖНОСТЬ
Центр Ci(3; 2)
Радиус = 1,4142135623731
ОПИСАННАЯ ОКРУЖНОСТЬ
Центр Co(2,5; 3,5)
Радиус = 3,53553390593274
МЕДИАНЫ ТРЕУГОЛЬНИКА
Медиана АM1 из вершины A:
Координаты M1(2,5; 3,5)
Длина AM1 = 3,53553390593274
ВЫСОТЫ ТРЕУГОЛЬНИКА
Высота AH1 из вершины A:
Координаты H1(3,48; 3,36)
Длина AH1 = 3,39411254969543
ответ: 119 см².
Объяснение:
Произведение ромба равно полупроизведению его диагоналей
S=(d1*d2)/2;
S=(14*17)/2 = 119 см².