
Столбы ставят перпендикулярно земле, а, следовательно, они параллельны между собой. Таким образом, получим, что ситуация, описанная в задаче, представляет собой следующую задачу:
Дана прямоугольная трапеция АВСD, основания которой BC = 9м и AD = 15м, а боковая сторона СD = 16м. Найдем сторону АВ (см. рис.).
Проведем СМ ⊥ AD, тогда ВС = АМ и АВ = СМ.
Получим прямоугольный треугольник СМD, у которого гипотенуза СD = 16 м, МD = АD - АМ = АD - ВС = 15- 9 = 6 (м).
По теореме Пифагора СМ² = СD² - МD² = 16² - 6² = 256 - 36 = 220 =
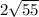
, откуда СМ =
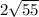
м.
Значит. и АВ =
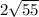
м.
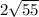
м
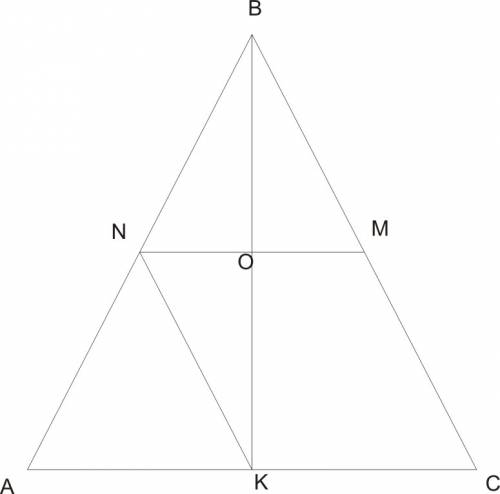
Δ АВС - равнобедренный
ВК = 30 см - биссектриса к основанию АС, она же и медиана Δ АВС ⇒ АК=КС
NM = 16 см - средняя линия II АС ⇒AN=NB
NK = ? - средняя линия II ВС
NM x ВК в т.О и деляться ей пополам, т.к. Δ NMB подобен Δ АВС по 3-м углам, ⇒ Δ NMB равнобедренный и ВО его высота, биссектриса и медиана.
ВО=ВК т.к. NM средняя линия Δ АВС
Получаем
NO=1/2NM= 16/2=8
OK=1/2ВК= 30/2=15
Δ NOK прямоугольный, т.к. уже доказано, что BO высота Δ NMB ⇒ <BON = 90°
<NOK - смежный и =180°-<BON = 90°
По теореме Пифагора находим NK - гипотенузу Δ NOK
NK=√(NO²+OK²) = √(8²+15²)=√(64+225)=√289=17 см
равны по 1 признаку(2 стороны и угол между ними)