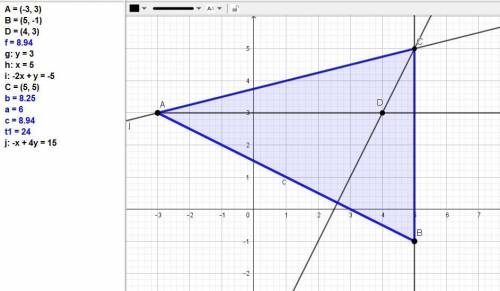
Уравнение АВ: (x-(-3))/(5-(-3) = (y-3)/(-1-3) или (x + 3)/8 = (y - 3)/(-4).
В общем виде x + 2y - 3 = 0.
Так как высота АД - горизонтальная линия, то уравнение стороны ВС:
х = 5.
В уравнении высоты СД как перпендикуляра к АВ коэффициенты А и В меняются на -В и А (скалярное произведение равно 0).
Уравнение СД: -2х + у + С = 0. Подставим координаты точки Д, через которую проходит высота: -2*4 + 1*3 + С = 0, отсюда С = 8-3 = 5.
Уравнение СД: -2х + у + 5 = 0.
Находим координаты точки С как точки пересечения стороны ВС и высоты СД:
{x = 5,
{-2х + у + 5 = 0, подставим х = 5.
-2*5 + у + 5 = 0, у = 10 - 5 = 5.
Точка С(5;5).
Уравнение АС: (x-(-3))/(5-(-3) = (y-3)/(5-3) или (x + 3)/8 = (y - 3)/2.
В общем виде x - 4y + 15 = 0.
1,6м 1,6м 3,2м АС= СВ
АО = ОС
Найти: АВ, АС, АО, ОВ
Решение:
АС = СВ = 3,2(см) (по условию)
АВ = АС + СВ = 3,2 + 3,2 = 6,4 (см),т.к. АС +СВ по усл.задачи.
АС = АО + ОС; АО=ОС (по условию), значит АО = ОС = АС : 2 = 3,2 : 2 = 1,6(см)
ОВ = ОС + СВ = 1,6 + 3,2 = 4,8 (см)