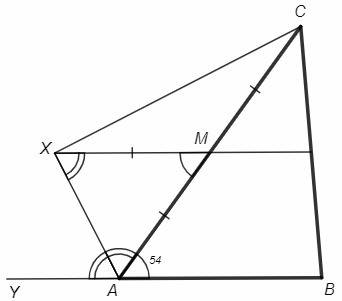
∠YAC - внешний угол, M - середина AC
∠YAX=∠MAX (AX - биссектриса ∠YAC)
∠YAX=∠MXA (накрест лежащие при XM||AB)
∠MAX=∠MXA => △XMA - равнобедренный, XM=MA
XM=MC, △XMC - равнобедренный => ∠XCA=∠MXC
∠XMA=2∠XCA (внешний угол равен сумме внутренних, не смежных с ним)
∠XMA=∠CAB=54 (накрест лежащие при XM||AB)
∠XCA=∠XMA/2 =54/2 =27
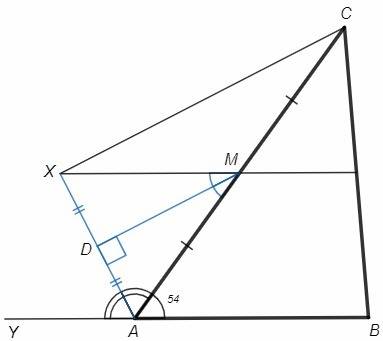
Или проведем биссектрису MD угла XMA. Биссектрисы внутренних углов при параллельных перпендикулярны, MD⊥AX. Биссектриса MD является высотой, следовательно и медианой. MD - средняя линия в треугольнике CAX, MD||CX. ∠XCA=∠DMA как соответственные. ∠XMA=∠CAB как накрест лежащие при XM||AB. ∠XCA=∠XMA/2=∠CAB/2=27
∠YAC - внешний угол, M - середина AC
∠YAX=∠MAX (AX - биссектриса ∠YAC)
∠YAX=∠MXA (накрест лежащие при XM||AB)
∠MAX=∠MXA => △XMA - равнобедренный, XM=MA
XM=MC, △XMC - равнобедренный => ∠XCA=∠MXC
∠XMA=2∠XCA (внешний угол равен сумме внутренних, не смежных с ним)
∠XMA=∠CAB=54 (накрест лежащие при XM||AB)
∠XCA=∠XMA/2 =54/2 =27
Или проведем биссектрису MD угла XMA. Биссектрисы внутренних углов при параллельных перпендикулярны, MD⊥AX. Биссектриса MD является высотой, следовательно и медианой. MD - средняя линия в треугольнике CAX, MD||CX. ∠XCA=∠DMA как соответственные. ∠XMA=∠CAB как накрест лежащие при XM||AB. ∠XCA=∠XMA/2=∠CAB/2=27


Гпржпше пс
Ил гөж жашжаштупддо һәм ул үҙенең һөҙөмтәләрен бирә торған булған һәм ул үҙенең һөҙөмтәләрен бирә ала ла бар ине һәм ул бик ҙур рәхмәт уларға ҡарата ярҙам күрһәтеү өсөн буйынса