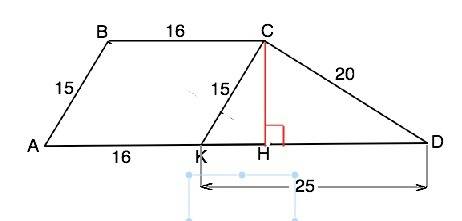
Обозначим вершины трапеции АВСD. Стороны: АВ=15, ВС=16, СD=20, AD=41. Из вершины С проведем СК параллельно АВ. Тогда АВСК - параллелограмм, и СК=15 см, АК=ВС=16 см, КD=AD-AK=25 см. Отношение сторон ∆ СКD=15:20:25, т.е. 3:4:5. ⇒ ∆ КСD - так называемый египетский, он прямоугольный. Площадь ∆ КСD=KC•CD:2=150 см². Тогда его высота СН=2S:KD=300:25=12 см (она же высота трапеции АВСD). Площадь трапеции равна половине произведения высоты на сумму оснований. S(ABCD)=CH•(BC+AD):2=12•57:2=342 см²
Подобных задач с полным и правильным ответом на сайте немало. При желании можно найти другие варианты решения.
S= (a+b) / 2 × h, где a и b - длины оснований, h - высота
h= 3 , a=10, b=3
S= (10+2) /2 × 3
S=6×3 = 18
Для нахождения периметра мы должны сначала найти длину боковой стороны трапеции. Так как трапеция равнобедренная, если опустить высоты из обоих тупых углов к противоположному основанию, мы получим РАВНЫЕ прямоугольные треугольники справа и слева и прямоугольник в середине. Нам нужно вычислить гипотенузу треугольников - это и будет боковая сторона трапеции.
Мы знаем длину одного из катетов : h=3, длина второго катета будет равняться разности оснований, делёной на 2. (10-2)/2=4.
Дальше вычисляем гипотенузу по теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
√( 3²+4²)=√25=5 - длина боковой стороны.
складываем боковые стороны и основания - получаем периметр.
P= 10+2+5+5 =22