Объяснение:
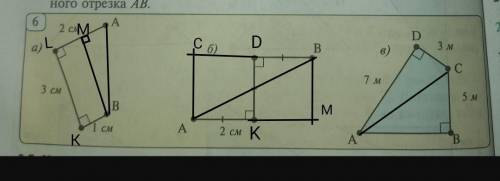
а)
Прямоугольная трапеция.
LM=KB=1см
МА=LA-LM=2-1=1см.
LK=MB=3см
∆MBA- прямоугольный треугольник.
По теореме Пифагора
АВ=√(МВ²+МА²)=√(3²+1²)=√(9+1)=√10 см
ответ: АВ=√10см
б)
Достроим прямоугольник
CD=AK=2см
CB=СD+DB=2+2=4см.
СА=DK=2см.
∆АСВ- прямоугольный треугольник
По теореме Пифагора
АВ=√(АС²+СВ²)=√(2²+4²)=√(4+16)=√20=
=2√5 см
ответ: АВ=2√5 см.
в)
∆АDC- прямоугольный треугольник
По теореме Пифагора
АС=√(АD²+DC²)=√(3²+7²)=√(9+49)=
=√58 см
∆АСВ- прямоугольный треугольник
По теореме Пифагора
АВ=√(АС²-СВ²)=√(58-5²)=√(58-25)=√33см
ответ: АВ=√33см
Если AB=BC то треугольник ABC — равнобедренный с основанием AC. Если AC=AD то треугольник ADC — равнобедренный с основанием CD. Так как углы при основании равнобедренного треугольника равны, то ∠BAC=∠BCA, ∠ADC=∠ACD. Далее ∠DAC=∠BCA как внутренние накрест лежащие при AD║BC и секущей AC.
Пусть ∠BAC=x, тогда ∠BAC=x, ∠DAC=x. Тогда ∠BAD=∠BAC+∠DAC=2x. Тогда ∠ADC=∠BAD=2x как углы при основании равнобедренной трапеции. Следовательно, ∠ACD=2x, ∠BCD=∠BCA+∠ACD=3x. По свойству равнобедренной трапеции имеем ∠BAD+∠BCD=180°. Составим уравнение: 2x+3x=180⇔x=36°
Значит, ∠BAD=2×36=72°, ∠BCD=3×36=108°.
ответ: 72° и 108°.
Объяснение: