по теореме косинусов зная угол в 120 градусов найдем основание треугольника:
х" = 36+36-2*36*(-1/2), = 72+36 = √108
так как угол между диагональю большей грани и основанием 60 градусов.
то в прямоугольном треугольника где катет высота призмы и основание треугольника ..высота треугольника равна: cos 30 = h/12√3 (катет лежайщий напротив угла в 30 градусов равен половине гипотенузы, сторона 6√3 лежит напротив этого угла), h = 18
площадь этой грани равна: S1 = 18*6√3 = 108√3.
S полн = 2Sосн + S1 + 2S2
S осн = 6*6*√3/2*2 = 9√3
S2 = 18*6 = 108
S полн = 2*9√3 + 108√3+2*108 = 126√3+216.
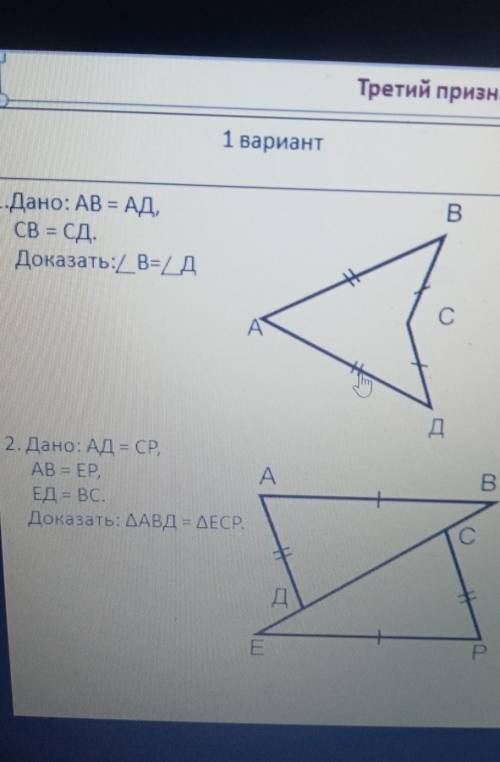
1. Проведём АС
Имеем АВ=АД, ВС=СД, АС - общая сторона, поэтому треугольники АВС и АДС равны по 3 теореме равенства треугольников.
Из равенства треугольников АВС и АДС имеем угол В равен углу Б
Доказано
2. ДВ=ДС+ВС, ЕС=ЕД+ДС, ДС - общая часть этих отрезков, ЕД=ВС, поэтому ДВ=ЕС.
Имеем ДВ=ЕС, АД=СР, АВ=ЕР, поэтому треугольники АВД и ЕСР равны по 3 теореме равенства треугольников.
Доказано