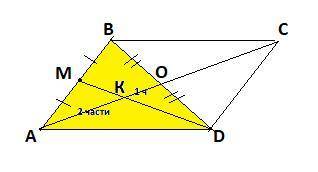
Диагональ АС параллелограмма АBCD равна 18см.Середина М стороны АВ соединена с вершиной D. Найдите отрезки, на которые делится диагональ АС отрезком DM.
Объяснение:
Проведем диагональ ВD, О-точка пересечения диагоналей . По свойству диагоналей параллелограмма АО=ОС=9 см.
Рассмотрим ΔАВD , АО-медиана ( тк. диагонали точкой пересечения делятся пополам) , MD- медиана ( т.к. М-середина по условию).
Пусть К-точка пересечения АО и МD.
По т. о точке пересечения медиан АО:КО=2:1 ⇒АО=9:3*2=6 (см)
Тогда КС=18-6=12 (см)
====================================
Медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины.
5√5см
Объяснение:
∆ABC- прямоугольный треугольник
По теореме Пифагора
АС=√(АВ²+ВС²)=√(16²+12²)=√(256+144)=
=√400=20см.
ОА=АС/2=20/2=10см.
∆FOA- прямоугольный треугольник.
По теореме Пифагора
FA=√(FO²+OA²)=√(10²+5²)=√125=5√5 см