1.В основании пирамиды SABCD лежит ромб. Высота пирамиды SA перпендикулярна основанию. Докажите, что SC перпендикулярно BD.
2.Длины сторон прямоугольника равны 16 и 12. Через точку О пересечения диагоналей прямоугольника проведен перпендикуляр к плоскости прямоугольника ОТ равный 24. Найдите расстояние от точки Т до вершин прямоугольника.
3.Дан прямоугольник АВСД. На стороне АВ построен двугранный угол КАВС, равный 30 градусам. АК перпендикулярна АВ, АК=2√3, АВ=4, АД=8. Найдите КС.
4.В основании пирамиды SABCD лежит ромб. Высота пирамиды SA перпендикулярна основанию. Найдите расстояние от точки S до прямой BD, если сторона ромба равна 6, SC=10, и треугольник АВС равносторонний.
5.В правильной четырёхугольной призме АВСДА1В1С1Д1 в основании лежит квадрат со стороной 15. Высота призмы равна 20. В призме проведено сечение проходящее через прямую Д1С1 перпендикулярно плоскости А1В1СД. Найдите периметр этого сечения.
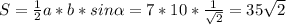 см²
см²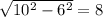 см. Рассмотрим другой прямоугольный треугольник, который сотворен диагональю (гипотенуза), высотой (катет) и вторым катетом, который лежитт на большем основанием трапеции, найдем его:
см. Рассмотрим другой прямоугольный треугольник, который сотворен диагональю (гипотенуза), высотой (катет) и вторым катетом, который лежитт на большем основанием трапеции, найдем его:  см. Найдем большее основание: 6+15=21см, меньшее: 15-6=9см.
см. Найдем большее основание: 6+15=21см, меньшее: 15-6=9см. 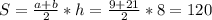 cм².
cм².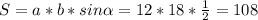 см²
см²
Решение: S=(a+b)делим на 2 и всё это умножаем на h-высоту.
из точки В к основанию АД проводим высоту, обозначим её точкой К, высота будет перпендикулярна СД. Образуется треугольник АВК, в котором угол при к равен 90 градусов. значит, в треугольнике АВК: АВ=8см, АК=5см ( т.к. большее основание равно 16см, меньше равно 6, следовательно 16-6=10-сумма длин двух катетов при большем основании, 10:2=5-длина одного катета в треугольнике при большем основании). Чтобы найти площадь трапеции, нам надо знать длину высоты ВК(или h) (по-другому это будет неизвестный катет в прямоугольном треугольнике)., а чтобы узнать длину высоты,используем теорему Пифагора c^2=a^2+b^2. из этой теоремы находим неизвестный катет---> a^2=c^2-b^2. подставляем теперь числа к этой формуле:
а^2=8^2 - 5^2
a^2=64-25
a^2=39
a=квадратный корень из 39-это высота h
теперь найдём площадь трапеции: S=(6+16)/2 и умножаем на квадратный корень из 39 = 11 умноженное на корень из 39
ответ:S=11 умноженное на корень из 39