1) с=√(а²+b²) = √(16+9) =5см.
Sinα = a/c = 0,8. α ≈ 53°.
Sinβ = b/c = 0,6. β ≈ 37°.
2) b=√(с²-а²) =√(169-144) =5см.
Sinα = a/c = 12/13 ≈ 0,923. α ≈ 67°.
Sinβ = b/c = 5/13 ≈ 0,385. β ≈ 23°.
3) α=30°, значит а=0,5·с = 20см (катет a против угла 30°).
b = √(c²-a²) = √(40²-20²) = 20√3.
β = 60°. (по сумме острых углов прямоугольного треугольника).
4) α=45°, значит β = 45°. а=b= 4см, с= √(а²+b²) = √32 = 4√2см.
5) α=60°, значит β = 30°. (по сумме острых углов прямоугольного треугольника).
с=2·b = 10см (катет b против угла 30°).
а = √(с²-b²)= √75 = 5√3см.
6) а=√(с²-b²)=√(100-36) = √64 = 8дм.
Sinα = a/c = 0,8. α ≈ 53°.
Sinβ = b/c = 0,6. β ≈ 37°.
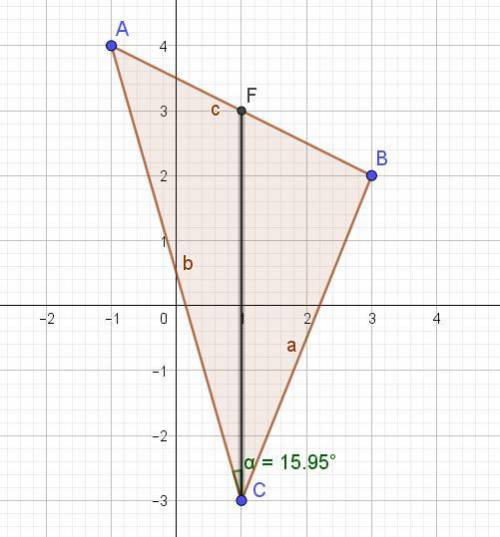
ответ: ∡ACF=arccos(3*√5/10)
Объяснение:
1. Найдем координату точки F. F- точка , которая делит пополам сторону АВ ( так как CF - медиана)
F = ( (Xa+Xb)/2 ; (Ya+Yb)/2) = ((-1+3)/2 ; (4+2)/2)= (1;3)
2. Найдем длину медианы CF:
CF=sqrt( (Xf-Xc)²+(Yf-Yc)²)= sqrt((1-1)²+ (3-(-3))²)=sqrt(0+9)=3
3. Найдем AF =sqrt ((Xf-Xa)² +(Yf-Ya)²)= sqrt ((1-(-1))²+(3-4)²)= sqrt(2²+1²)=√5
4. Найдем АС=sqrt((Xc-Xa)²+(Yc-Ya)²)=sqrt((1-(-1))²+(-3-(-4))²)=sqrt(2²+1²)=√5
=> ΔACF- равнобедренный (AС=AF).
=>cos ∡ACF= 3/√5/2=3*√5/10
∡ACF=arccos(3*√5/10)
Объяснение:
а.) гострокутний
это не точно